题目内容
设集合A={x|1<x<4},B={x|x 2-2x-3≤0},则A∩(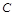 RB)=( )
RB)=( )
A.(1,4) B.(3,4) C.(1,3) D.(1,2)
B
解析试题分析:因为A={x|1<x<4},B={x|x 2-2x-3≤0}={x|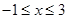 },所以
},所以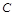 RB={x|3<x<4}, A∩(
RB={x|3<x<4}, A∩(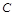 RB)=(3,4).故选B。
RB)=(3,4).故选B。
考点:本题主要考查集合的运算,简单不等式解法。
点评:简单题,直接按交集的定义计算。注意交集是两集合中所有相同元素构成的集合。明确集合中的元素是关键。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设集合 ,
,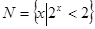 ,则
,则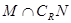 等于( )
等于( )
A.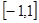 | B. | C.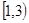 | D.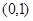 |
设函数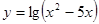 的定义域为M,函数
的定义域为M,函数 的定义域为N,则( )
的定义域为N,则( )
| A.M∪N=R | B.M="N" | C.M N N | D.M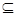 N N |
符号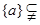
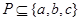 的集合P的个数是 ( )
的集合P的个数是 ( )
| A.2 | B.3 | C.4 | D.5 |
已知全集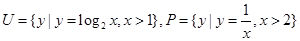 ,则
,则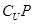 =( )
=( )
A.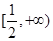 | B.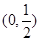 |
C.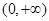 | D.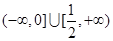 |
设全集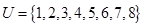 ,集合
,集合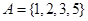 ,
,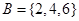 ,则图中的阴影部分表示的集合为( )
,则图中的阴影部分表示的集合为( )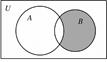
A.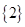 | B.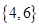 | C.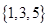 | D.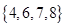 |
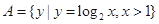 ,
,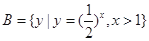 ,则
,则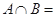 ( ).
( ).
A.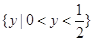 | B.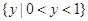 | C. | D.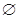 |
已知全集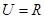 ,集合
,集合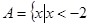 或
或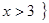 ,集合
,集合 ,那么集合(
,那么集合(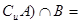 ( )
( )
A. | B.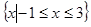 |
C.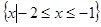 | D.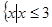 或 或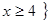 |
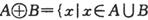 ,且
,且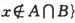 .已知两个开区间M=(a,b),N=(c,d),其中a、b、c、d满足
.已知两个开区间M=(a,b),N=(c,d),其中a、b、c、d满足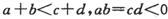 ,则
,则 =
= 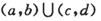 B.
B.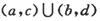
 D.
D.