题目内容
已知函数f(x)=-x2+2ax+1-a在x∈[0,1]时有最大值2,求a的值.
【答案】
a=2,或a=-1.
【解析】
试题分析:解:原函数的对称轴为x=a,开口向下,①当a<0时,f(x)在[0,1]上单调递减,∴f(x)的最大值为f(0)=1-a=2,∴a=-1<0,∴a=-1符合题意,②当0≤a≤1时,f(x)的最大值为f(a)=-a2+2a2+1-a=a2-a+1=2,∴a=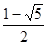 或a=
或a=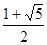 ?[0,1],∴不合题意,无解,③当a>1时,f(x)在[0,1]上单调递增,∴f(x)的最大值为f(1)=-1+2a+1-a=a=2>1,∴a=2符合题意,综①②③得a=-1或a=2
?[0,1],∴不合题意,无解,③当a>1时,f(x)在[0,1]上单调递增,∴f(x)的最大值为f(1)=-1+2a+1-a=a=2>1,∴a=2符合题意,综①②③得a=-1或a=2
考点:二次函数求最值问题
点评:本题考察二次函数求最值问题,注意对称轴与区间的位置关系,当对称轴于区间的位置关系不确定时,须分类讨论,从而得到原函数的单调性,进而可以求最值

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有