题目内容
设等差数列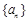 的前
的前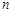 项和为
项和为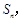 且
且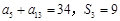 .
.
(1)求数列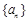 的通项公式及前
的通项公式及前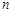 项和公式;
项和公式;
(2)设数列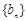 的通项公式为
的通项公式为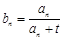 ,问: 是否存在正整数t,使得
,问: 是否存在正整数t,使得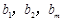
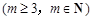 成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
【答案】
(1)故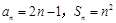 . (2)当
. (2)当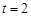 时,
时,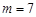 ;当
;当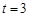 时,
时,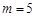 ;当
;当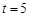 时,
时,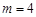 .
.
【解析】本试题考查了数列的概念和求和的运用。
解(1)设等差数列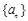 的公差为d. 由已知得
的公差为d. 由已知得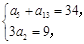 ………………2分
………………2分
即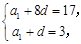 解得
解得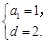 ……………………5分.
……………………5分.
故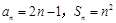 . ………9分
. ………9分
(2)由(1)知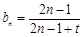 .要使
.要使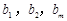 成等差数列,必须
成等差数列,必须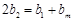 ,即
,即 ,……8分.整理得
,……8分.整理得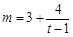 , ……………11分
, ……………11分
因为m,t为正整数,所以t只能取2,3,5.
当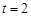 时,
时,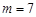 ;当
;当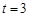 时,
时,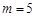 ;当
;当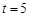 时,
时,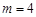 .
.
故存在正整数t,使得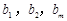 成等差数列.
成等差数列.

练习册系列答案
相关题目
 的前
的前 项和为
项和为 且满足
且满足 则
则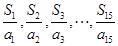 中最大的项为( )
中最大的项为( ) B.
B. C.
C. D.
D.
 的前
的前 项和为
项和为 ,已知
,已知 ,
, ,则
,则 .
.