题目内容
（文）已知三棱锥A-BCD的所有棱长都相等，则直线AB与平面BCD所成角的大小为
arccos
| ||
| 3 |
arccos
（用反三角函数表示）．
| ||
| 3 |
分析：先确定直线AB与平面BCD所成角，再用余弦函数进行计算，即可得到结论．
解答：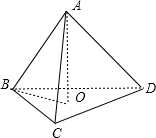
解：设三棱锥A-BCD的所有棱长都为a，过A作AO⊥面BCD，垂足为O，则∠ABO为直线AB与平面BCD所成角
∵三棱锥A-BCD的所有棱长都相等
∴O是△BCD的中心
∴OB=
a
∴cos∠ABO=
=
∴∠ABO=arccos
∴直线AB与平面BCD所成角的大小为arccos
故答案为：arccos
解：设三棱锥A-BCD的所有棱长都为a，过A作AO⊥面BCD，垂足为O，则∠ABO为直线AB与平面BCD所成角∵三棱锥A-BCD的所有棱长都相等
∴O是△BCD的中心
∴OB=
| ||
| 3 |
∴cos∠ABO=
| OB |
| AB |
| ||
| 3 |
∴∠ABO=arccos
| ||
| 3 |
∴直线AB与平面BCD所成角的大小为arccos
| ||
| 3 |
故答案为：arccos
| ||
| 3 |
点评：本题考查线面角，解题的关键是正确作出线面角，属于中档题．
练习册系列答案
相关题目
B．
C．
D．
，1，
，则PS的长度为（ ）
C．
D．3
，1，
，则PS的长度为（ ）
C．
D．3