Question

设函数f(x)满足f()=f(x)，f(x)=f(2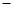x)，且当时，f(x)=x³.又函数g(x)=|xcos|，则函数h(x)=g(x)-f(x)在上的零点个数为(    )

A.5                  B.6              C.7             D.8

 

Answer 1

【答案】

B

【解析】解：因为解：因为当x∈[0，1]时，f（x）=x³．

所以当x∈[1，2]时2-x∈[0，1]，f（x）=f（2-x）=（2-x）³，

当x∈[0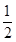，]时，g（x）=xcos（πx）；当x∈时，g（x）=-xcosπx，

注意到函数f（x）、g（x）都是偶函数，且f（0）=g（0），f（1）=g（1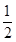），g（）=g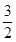（）=0作出函数f（x）、g（x）的大致图象，函数h（x）除了0、1这两个零点之外，分别在区间

上各有一个零点，共有6个零点，故选B