题目内容
已知命题p:在x∈[1,2]内,不等式x2+ax-2>0恒成立;命题q:函数f(x)=log| 1 | 3 |
分析:利用复合命题真假的判断方法求解实数a的取值范围是解决本题的关键.首先要确定出命题p,q为真的字母a的取值范围,利用恒成立问题的分离变量方法得出命题p为真的a的范围;利用复合函数单调性的方法得出命题q为真的a的范围,注意对数函数定义域的意识.
解答:解:∵x∈[1,2]时,不等式x2+ax-2>0恒成立
∴a>
=
-x在x∈[1,2]上恒成立,
令g(x)=
-x,则g(x)在[1,2]上是减函数,
∴g(x)max=g(1)=1,∴a>1.即若命题p真,则a>1;
又∵函数f(x)=log
(x2-2ax+3a)是区间[1,+∞)上的减函数,
∴
∴
∴-1<a≤1.即若命题q真,则-1<a≤1.
若命题“p?q”是真命题,则有p真q假或p假q真或p,q均为真命题,
若p真q假,则有a>1,若p假q真,则有-1<a≤1,若p,q均为真命题,不存在a;
综上可得实数a的取值范围是a>-1.
∴a>
| 2-x2 |
| x |
| 2 |
| x |
令g(x)=
| 2 |
| x |
∴g(x)max=g(1)=1,∴a>1.即若命题p真,则a>1;
又∵函数f(x)=log
| 1 |
| 3 |
∴
|
∴
|
若命题“p?q”是真命题,则有p真q假或p假q真或p,q均为真命题,
若p真q假,则有a>1,若p假q真,则有-1<a≤1,若p,q均为真命题,不存在a;
综上可得实数a的取值范围是a>-1.
点评:本题考查复合命题真假与简单命题真假之间的关系,或形式的命题为真只要二者都不为假命题即可,因此要分三种情况进行确定.首先要确定出这两个简单命题分别为真的a的范围,这是解决本题的突破口,考查学生的转化与化归能力.

练习册系列答案
相关题目
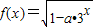 在x∈(-∞,0]上有意义,命题q:函数y=lg(ax2-x+a)的定义域为R.如果p和q有且仅有一个正确,则a的取值范围 .
在x∈(-∞,0]上有意义,命题q:函数y=lg(ax2-x+a)的定义域为R.如果p和q有且仅有一个正确,则a的取值范围 .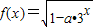 在x∈(-∞,0]上有意义,命题q:函数y=lg(ax2-x+a)的定义域为R.如果p和q有且仅有一个正确,则a的取值范围 .
在x∈(-∞,0]上有意义,命题q:函数y=lg(ax2-x+a)的定义域为R.如果p和q有且仅有一个正确,则a的取值范围 .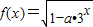 在x∈(-∞,0]上有意义,命题q:函数y=lg(ax2-x+a)的定义域为R.如果p和q有且仅有一个正确,则a的取值范围 .
在x∈(-∞,0]上有意义,命题q:函数y=lg(ax2-x+a)的定义域为R.如果p和q有且仅有一个正确,则a的取值范围 .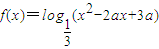 是区间[1,+∞)上的减函数.若命题“p?q”是真命题,求实数a的取值范围.
是区间[1,+∞)上的减函数.若命题“p?q”是真命题,求实数a的取值范围.