题目内容
过点P(-3,-2)且与圆:x2+y2+2x-4y+1=0相切的直线方程是 .
x=-3或3x-4y+1=0
解析试题分析:当切线的斜率不存在时,x=-3满足题意;
当切线的斜率存在时,设直线方程为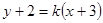 ,因为直线与圆相切,所以
,因为直线与圆相切,所以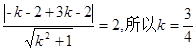 ,所以切线方程为3x-4y+1=0。
,所以切线方程为3x-4y+1=0。
综上知:满足条件的切线方程为x=-3或3x-4y+1=0。
考点:圆的切线的性质;圆的一般式方程;直线方程的点斜式;点到直线的距离公式。
点评:在设直线方程的点斜式时要注意讨论斜率是否存在。

练习册系列答案
相关题目
 ,
, ,则直线
,则直线 的倾斜角是 .
的倾斜角是 . 为圆
为圆 的弦的中点,则该弦所在直线的方程是__ __;
的弦的中点,则该弦所在直线的方程是__ __; 且在
且在 轴的截距为
轴的截距为 的直线方程是____________________.
的直线方程是____________________.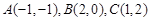 ,则△ABC中AB边上的高所在的直线方程为
,则△ABC中AB边上的高所在的直线方程为 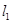 :2x+3y-1=0,
:2x+3y-1=0,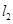 :Ax-6y+C=0,当A,C满足条件:__________时,
:Ax-6y+C=0,当A,C满足条件:__________时,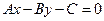 ,不经过第 象限
,不经过第 象限