题目内容
已知f(x)的定义域为(0,+∞),且满足f(2)=1,f(xy)=f(x)+f(y),又当x2>x1>0时,f(x2)>f(x1).
(1)求f(1)、f(4)、f(8)的值;
(2)若有f(x)+f(x-2)≤3成立,求x的取值范围.
【答案】
(1)0,2,3(2)(2,4].
【解析】
试题分析:解:(1)f(1)=f(1)+f(1),∴f(1)=0,
f(4)=f(2)+f(2)=1+1=2,
f(8)=f(2)+f(4)=2+1=3. 6
(2)∵f(x)+f(x-2)≤3,∴f[x(x-2)]≤f(8),
又∵对于函数f(x)有x2>x1>0时f(x2)>f(x1),
∴f(x)在(0,+∞)上为增函数. 10
∴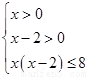 ?2<x≤4.
?2<x≤4.
∴x的取值范围为(2,4]. 14
考点:抽象函数
点评:主要是考查了赋值法来求解函数的值,以及单调性的判定,属于基础题。

练习册系列答案
相关题目

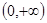 ,若对任意x1>0,x2>0,均有f(x1+x2)=f(x1)+
f(x2),且f(8)=3,则f(2)=
,若对任意x1>0,x2>0,均有f(x1+x2)=f(x1)+
f(x2),且f(8)=3,则f(2)= C.
C. D.
D.