题目内容
 如图,已知四面体A-BCD的四个顶点都在球M的球面上,BD=2,其余棱长均为
如图,已知四面体A-BCD的四个顶点都在球M的球面上,BD=2,其余棱长均为| 2 |
| π |
| 2 |
| π |
| 2 |
分析:取BD的中点O,连结OA、OC,由勾股定理的逆定理,算出△ABD是以BD为斜边的等腰直角三角形,得OA=
BD=1,同理得出OC=
BD=1,从而OA=OB=OC=OD=1,得到球M的球心与BD中点O重合.在△AOC算出∠AOC=90°,利用球面距离计算公式即可算出此A、C的球面距离.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解: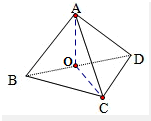 取BD的中点O,连结OA、OC,
取BD的中点O,连结OA、OC,
∵△ABD中,AB=AD=
,BD=2
∴△ABD是以BD为斜边的等腰直角三角形,可得OA=
BD=1,
同理可得:△BCD中,OC=
BD=1
因此OA=OB=OC=OD=1,可得以O为球心、1为半径的球面上,
即球M的球心与BD中点O重合,
∵△AOC中,AO=OC=1,AC=
∴△AOC是以O为斜边的等腰直角三角形,得∠AOC=90°
因此A、C的球面距离等于
=
故答案为:
 取BD的中点O,连结OA、OC,
取BD的中点O,连结OA、OC,∵△ABD中,AB=AD=
| 2 |
∴△ABD是以BD为斜边的等腰直角三角形,可得OA=
| 1 |
| 2 |
同理可得:△BCD中,OC=
| 1 |
| 2 |
因此OA=OB=OC=OD=1,可得以O为球心、1为半径的球面上,
即球M的球心与BD中点O重合,
∵△AOC中,AO=OC=1,AC=
| 2 |
∴△AOC是以O为斜边的等腰直角三角形,得∠AOC=90°
因此A、C的球面距离等于
| 90π×1 |
| 180 |
| π |
| 2 |
故答案为:
| π |
| 2 |
点评:本题在三棱锥中求外接球面上两点的球面距离,着重考查了勾股定理的逆定理、多面体的外接球和球面距离公式及其计算等知识,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
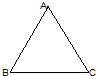 已知四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),则其侧视图的面积是( )
已知四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),则其侧视图的面积是( )A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )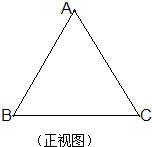 已知四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),则其侧视图的面积是
已知四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),则其侧视图的面积是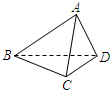 如图,已知正四面体ABCD的棱长为3cm.
如图,已知正四面体ABCD的棱长为3cm.