题目内容
已知椭圆C的中心在原点,F1、F2分别为它的左、右焦点,直线x=4为它的一条准线,又知椭圆C上存在点M,使得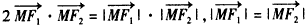 ,
,
(1)求椭圆C的方程;
(2)若PQ为过椭圆焦点F2的弦,且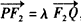 ,求△PF1Q的内切圆面积最大时实数λ的值.
,求△PF1Q的内切圆面积最大时实数λ的值.
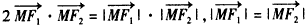 ,
,(1)求椭圆C的方程;
(2)若PQ为过椭圆焦点F2的弦,且
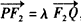 ,求△PF1Q的内切圆面积最大时实数λ的值.
,求△PF1Q的内切圆面积最大时实数λ的值.解:(1)据题意,设椭圆C的方程为 ,
, ,
,
∵直线x=4为椭圆C的准线,
∴ ,
,
又 ,
,
∴M为椭圆C短轴上的顶点,
∵ ,
,
∴ ,
,
∴∠F1MF2=60°,则△F1MF2为等边三角形,
∴ , 故a2=4c=2a,
, 故a2=4c=2a,
∴a=2,c=1,
∴b2=a2-c2=22-12=3,
∴椭圆C的方程为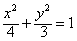 。
。
(2)显然直线PQ不与x轴重合,当PQ与x轴垂直,
即直线PQ斜率不存在时, ,
,
∴ ;
;
当直线PQ斜率存在时,设它的斜率为k,则直线PQ的方程为y=k(x-1)(k≠0),
代入椭圆C的方程,消去x并整理得:(4k2+3)y2+6ky-9k2=0,
Δ=36k2+36k2(4k2+3)>0,
设P(x1,y1),Q(x2,y2),则 ,
,
∴ ,
,
设4k2+3=t,则t>3,此时 ,
,
又∵F1到直线PQ的距离 ,
,
∴ ,
,
 ,
,
∴0< <3,
<3,
综上,直线PQ与x轴垂直时,△PF1Q的面积最大,且最大面积为3,
设△PF1Q的内切圆半径为r,
则
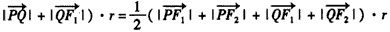 =4r,
=4r,
∴ ,即
,即 时,△PF1Q的内切圆面积最大,
时,△PF1Q的内切圆面积最大,
此时直线PQ的斜率不存在,直线PQ与x轴垂直,
∴ ,即λ=1。
,即λ=1。
 ,
, ,
,∵直线x=4为椭圆C的准线,
∴
 ,
,又
 ,
,∴M为椭圆C短轴上的顶点,
∵
 ,
,∴
 ,
,∴∠F1MF2=60°,则△F1MF2为等边三角形,
∴
 , 故a2=4c=2a,
, 故a2=4c=2a,∴a=2,c=1,
∴b2=a2-c2=22-12=3,
∴椭圆C的方程为
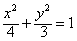 。
。(2)显然直线PQ不与x轴重合,当PQ与x轴垂直,
即直线PQ斜率不存在时,
 ,
,∴
 ;
;当直线PQ斜率存在时,设它的斜率为k,则直线PQ的方程为y=k(x-1)(k≠0),
代入椭圆C的方程,消去x并整理得:(4k2+3)y2+6ky-9k2=0,
Δ=36k2+36k2(4k2+3)>0,
设P(x1,y1),Q(x2,y2),则
 ,
,∴
 ,
,设4k2+3=t,则t>3,此时
 ,
,又∵F1到直线PQ的距离
 ,
,∴
 ,
, ,
,∴0<
 <3,
<3,综上,直线PQ与x轴垂直时,△PF1Q的面积最大,且最大面积为3,
设△PF1Q的内切圆半径为r,
则

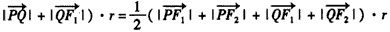 =4r,
=4r,∴
 ,即
,即 时,△PF1Q的内切圆面积最大,
时,△PF1Q的内切圆面积最大,此时直线PQ的斜率不存在,直线PQ与x轴垂直,
∴
 ,即λ=1。
,即λ=1。
练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目

 。
。