题目内容
某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,记作y=f(t),下面是某日水深的数据:| t(小时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
(1)求函数y=f(t)的近似表达式;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的.某船吃水深度(船底离水面的距离)为6.5米,如果该船希望在同一天内安全进出港,请问:它至多能在港内停留多长时间?
分析:(1)由表格得到三角函数的周期,利用周期公式求出ω;利用A等于最大值减去最小值和的一半;b等于最大值加上最小值的差的一半,求出f(t).
(2)将实际问题转化为 不等式,列出不等式,结合三角函数的图象求出不等式的解集.
(2)将实际问题转化为 不等式,列出不等式,结合三角函数的图象求出不等式的解集.
解答:解:(1)由题知:周期T=12,故ω=
,
又b=10,A=3,∴y=3sin
t+10.
(2)由题知:y=3sin
t+10≥5+6.5,∴sin
t≥
∴1≤t≤5或13≤t≤17
如图:
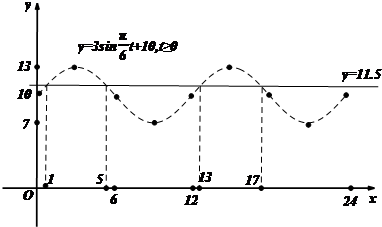
当该船1时入港,17时出港,停留时间最长,为16小时.
| π |
| 6 |
又b=10,A=3,∴y=3sin
| π |
| 6 |
(2)由题知:y=3sin
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
|
如图:

当该船1时入港,17时出港,停留时间最长,为16小时.
点评:本题考查据三角函数的性质求三角函数的解析式、结合三角函数的图象求三角不等式.

练习册系列答案
相关题目
某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,记作y=f(t),下面是某日水深的数据:
经长期观察:y=f(t)的曲线可近似看成函数y=Asinωt+b的图象(A>0,ω>0).
(1)求函数y=f(t)的近似表达式;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的.某船吃水深度(船底离水面的距离)为6.5米,如果该船希望在同一天内安全进出港,请问:它至多能在港内停留多长时间?
| t(小时) | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | |
| y(米) | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
(1)求函数y=f(t)的近似表达式;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的.某船吃水深度(船底离水面的距离)为6.5米,如果该船希望在同一天内安全进出港,请问:它至多能在港内停留多长时间?
某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,记作y=f(t),下面是某日水深的数据:
经长期观察:y=f(t)的曲线可近似看成函数y=Asinωt+b的图象(A>0,ω>0).
(1)求函数y=f(t)的近似表达式;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的.某船吃水深度(船底离水面的距离)为6.5米,如果该船希望在同一天内安全进出港,请问:它至多能在港内停留多长时间?
| t(小时) | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | |
| y(米) | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
(1)求函数y=f(t)的近似表达式;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的.某船吃水深度(船底离水面的距离)为6.5米,如果该船希望在同一天内安全进出港,请问:它至多能在港内停留多长时间?
某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,记作y=f(t),下面是某日水深的数据:
经长期观察:y=f(t)的曲线可近似看成函数y=Asinωt+b的图象(A>0,ω>0).
(1)求函数y=f(t)的近似表达式;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的.某船吃水深度(船底离水面的距离)为6.5米,如果该船希望在同一天内安全进出港,请问:它至多能在港内停留多长时间?
| t(小时) | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | |
| y(米) | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
(1)求函数y=f(t)的近似表达式;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的.某船吃水深度(船底离水面的距离)为6.5米,如果该船希望在同一天内安全进出港,请问:它至多能在港内停留多长时间?
某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,记作y=f(t),下面是某日水深的数据:
经长期观察:y=f(t)的曲线可近似看成函数y=Asinωt+b的图象(A>0,ω>0).
(1)求函数y=f(t)的近似表达式;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的.某船吃水深度(船底离水面的距离)为6.5米,如果该船希望在同一天内安全进出港,请问:它至多能在港内停留多长时间?
| t(小时) | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | |
| y(米) | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
(1)求函数y=f(t)的近似表达式;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的.某船吃水深度(船底离水面的距离)为6.5米,如果该船希望在同一天内安全进出港,请问:它至多能在港内停留多长时间?