题目内容
已知等比数{an}，a1=1，a4=8，在an与an+1两项之间依次插入2n-1个正整数，得到数列{bn}，即a1，1，a2，2，3，a3，4，5，6，7，a4，8，9，10，11，12，13，14，15，a5，…则数列{bn}的前2013项之和S2013= （用数字作答）．
【答案】分析：在数列{bn}中，到an项共有=n+（1+2+…+2n-2）=n+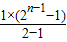
=2n-1+n-1项，即为f（n）（n≥2），因此判断出共含有an的项数，进而即可得出S2013．
解答：解：在数列{bn}中，到an项共有=n+（1+2+…+2n-2）=n+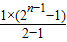
=2n-1+n-1项，即为f（n）（n≥2）．
则f（11）=210+11-1=1034，f（12）=211+12-1=2059．
设等比数{an}的公比为q，由a1=1，a4=8，得1×q3=8，解得q=2，
因此S2013=a1+a2+…+a10+a11+1+2+3+…+2002=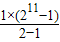
+
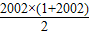=2007050．
故答案为2007050．
点评：熟练掌握等差数列和等比数列的前n项和公式及由已知判断出共含有an的项数是解题的关键．
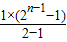=2n-1+n-1项，即为f（n）（n≥2），因此判断出共含有an的项数，进而即可得出S2013．解答：解：在数列{bn}中，到an项共有=n+（1+2+…+2n-2）=n+
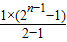=2n-1+n-1项，即为f（n）（n≥2）．则f（11）=210+11-1=1034，f（12）=211+12-1=2059．
设等比数{an}的公比为q，由a1=1，a4=8，得1×q3=8，解得q=2，
因此S2013=a1+a2+…+a10+a11+1+2+3+…+2002=
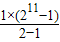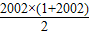+=2007050．故答案为2007050．
点评：熟练掌握等差数列和等比数列的前n项和公式及由已知判断出共含有an的项数是解题的关键．
练习册系列答案
相关题目