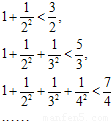题目内容
观察以下不等式
可归纳出对大于1的正整数n成立的一个不等式1+
+
+…
<f(n),则不等式右端f(n)的表达式应为
|
可归纳出对大于1的正整数n成立的一个不等式1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
f(n)=
(n≥2)
| 2n-1 |
| n |
f(n)=
(n≥2)
.| 2n-1 |
| n |
分析:根据已知中1+
<
,,1+
+
<
,…我们分析左边式子中的数是连续正整数平方的倒数和,右边分式中的分子是奇数,分母是正整数,归纳分析后,即可得到答案.
| 1 |
| 2 2 |
| 3 |
| 2 |
| 1 |
| 2 2 |
| 1 |
| 3 2 |
| 5 |
| 3 |
解答:解:由已知中的不等式
1+
<
,,1+
+
<
,…
我们分析左边式子中的数是连续正整数平方的倒数和,
右边分式中的分子是奇数2n-1,分母是正整数n,
即 1+
+
+…
<
,(n≥2),
故答案为:f(n)=
,(n≥2).
1+
| 1 |
| 2 2 |
| 3 |
| 2 |
| 1 |
| 2 2 |
| 1 |
| 3 2 |
| 5 |
| 3 |
我们分析左边式子中的数是连续正整数平方的倒数和,
右边分式中的分子是奇数2n-1,分母是正整数n,
即 1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 2n-1 |
| n |
故答案为:f(n)=
| 2n-1 |
| n |
点评:本小题主要考查归纳推理、数列等基础知识,考查运算归纳能力,考查分析问题和解决问题的能力.属于基础题.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 观察以下不等式可归纳出对大于1的正整数n成立的一个不等式1+
观察以下不等式可归纳出对大于1的正整数n成立的一个不等式1+
 ,则不等式右端
,则不等式右端 的表达式应为_________
的表达式应为_________
 ,则不等式右端
,则不等式右端 的表达式应为 *** .
的表达式应为 *** . …
… <f(n),则不等式右端f(n)的表达式应为 .
<f(n),则不等式右端f(n)的表达式应为 .