题目内容
在体积为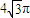 的球的表面上有A,B,C三点,
的球的表面上有A,B,C三点,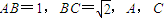 两点的球面距离为
两点的球面距离为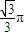 ,则球心到平面ABC的距离为 .
,则球心到平面ABC的距离为 .
【答案】分析:根据球的体积,首先就要先计算出球的半径.再根据A、C两点的球面距离,可求得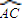 所对的圆心角的度数,进而根据余弦定理可得线段AC的长度为
所对的圆心角的度数,进而根据余弦定理可得线段AC的长度为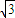 ,所以△ABC为直角三角形,所以线段AC的中点即为ABC所在平面的小圆圆心,进而可得球心到平面ABC的距离.
,所以△ABC为直角三角形,所以线段AC的中点即为ABC所在平面的小圆圆心,进而可得球心到平面ABC的距离.
解答:解析:设球的半径为R,则 ,
,
∴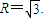
设A、C两点对球心张角为θ,则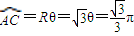 ,
,
∴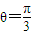 ,
,
∴由余弦定理可得: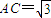 ,
,
∴AC为ABC所在平面的小圆的直径,
∴∠ABC=90°,
设ABC所在平面的小圆圆心为O',则球心到平面ABC的距离为d=OO'=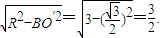
点评:本小题主要考查立体几何球面距离及点到面的距离.
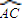 所对的圆心角的度数,进而根据余弦定理可得线段AC的长度为
所对的圆心角的度数,进而根据余弦定理可得线段AC的长度为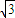 ,所以△ABC为直角三角形,所以线段AC的中点即为ABC所在平面的小圆圆心,进而可得球心到平面ABC的距离.
,所以△ABC为直角三角形,所以线段AC的中点即为ABC所在平面的小圆圆心,进而可得球心到平面ABC的距离.解答:解析:设球的半径为R,则
 ,
,∴
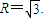
设A、C两点对球心张角为θ,则
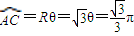 ,
,∴
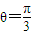 ,
,∴由余弦定理可得:
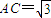 ,
,∴AC为ABC所在平面的小圆的直径,
∴∠ABC=90°,
设ABC所在平面的小圆圆心为O',则球心到平面ABC的距离为d=OO'=
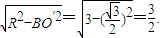
点评:本小题主要考查立体几何球面距离及点到面的距离.

练习册系列答案
相关题目
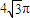 的球的表面上有A,B,C三点,
的球的表面上有A,B,C三点,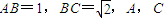 两点的球面距离为
两点的球面距离为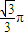 ,则球心到平面ABC的距离为 .
,则球心到平面ABC的距离为 .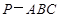 的四个顶点都在体积为
的四个顶点都在体积为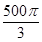 的球的表面上,底面ABC所在的小圆面积为16π,则该三棱锥的高的最大值为( )
的球的表面上,底面ABC所在的小圆面积为16π,则该三棱锥的高的最大值为( )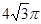 的球的表面上有A,B,C三点,AB=1,BC=
的球的表面上有A,B,C三点,AB=1,BC=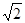 ,A,C两点的球面距离为
,A,C两点的球面距离为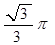 ,则球心到平面ABC的距离为
( )
,则球心到平面ABC的距离为
( )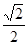 B.
B.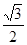 C.
C.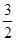 D.1
D.1 的球的表面上有A、B、C三点,
的球的表面上有A、B、C三点, ,A、C两点的球面距离为
,A、C两点的球面距离为 ,则球心到平面ABC的距离为
。
,则球心到平面ABC的距离为
。