题目内容
过坐标原点与曲线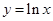 相切的直线方程为 .
相切的直线方程为 .
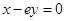
解析试题分析:设切点坐标为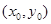 ,∵
,∵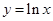 ,∴
,∴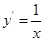 ,∴
,∴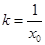 ,∴切线方程为
,∴切线方程为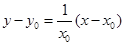 ,又∵
,又∵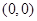 在切线上,∴
在切线上,∴ 即
即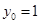 ,又∵
,又∵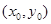 在曲线
在曲线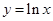 上,∴
上,∴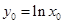 ,∴
,∴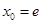 ,∴切线方程为
,∴切线方程为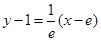 即
即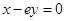 .
.
考点:过点求切线.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
题目内容
过坐标原点与曲线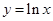 相切的直线方程为 .
相切的直线方程为 .
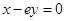
解析试题分析:设切点坐标为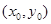 ,∵
,∵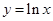 ,∴
,∴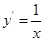 ,∴
,∴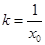 ,∴切线方程为
,∴切线方程为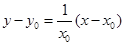 ,又∵
,又∵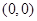 在切线上,∴
在切线上,∴ 即
即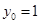 ,又∵
,又∵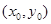 在曲线
在曲线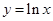 上,∴
上,∴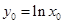 ,∴
,∴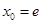 ,∴切线方程为
,∴切线方程为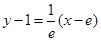 即
即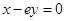 .
.
考点:过点求切线.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案