题目内容
某海域有A、B两个岛屿,B岛在A岛正东4海里处.经多年观察研究发现,某种鱼群洄游的路线是曲线C,曾有渔船在距A岛、B岛距离和为8海里处发现过鱼群.以A、B所在直线为x轴,AB的垂直平分线为y轴建立平面直角坐标系.(1)求曲线C的标准方程;
(2)某日,研究人员在A、B两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),A、B两岛收到鱼群在P处反射信号的时间比为5:3,问你能否确定P处的位置(即点P的坐标)?

【答案】分析:(1)根据椭圆的定义,由题意知曲线C是以A、B为焦点且长轴长为8的椭圆,又2c=4,从而得出a,b的值即可得到曲线C的方程;
(2)由于A、B两岛收到鱼群发射信号的时间比为5:3,因此设此时距A、B两岛的距离分别比为5:3,即鱼群分别距A、B两岛的距离为5海里和3海里.再设P(x,y),B(2,0),由|PB|=3,及椭圆的方程列出方程组即可解出点P的坐标.
解答:解:(1)由题意知曲线C是以A、B为焦点且长轴长为8的椭圆 (3分)
又2c=4,则c=2,a=4,故 (5分)
(5分)
所以曲线C的方程是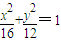 (6分)
(6分)
(2)由于A、B两岛收到鱼群发射信号的时间比为5:3,
因此设此时距A、B两岛的距离分别比为5:3(7分)
即鱼群分别距A、B两岛的距离为5海里和3海里. (8分)
设P(x,y),B(2,0),由|PB|=3,
∴ ,(10分)∴
,(10分)∴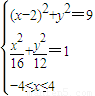 ,(12分)
,(12分)
∴x=2,y=±3(13分).
∴点P的坐标为(2,3)或(2,-3)(14分).
点评:本题考查椭圆问题在生产实际中的具体应用,涉及到椭圆方程的求法,椭圆的简单性质,椭圆的直线方程的关系,解题时要认真审题,注意转化思想的灵活运用.
(2)由于A、B两岛收到鱼群发射信号的时间比为5:3,因此设此时距A、B两岛的距离分别比为5:3,即鱼群分别距A、B两岛的距离为5海里和3海里.再设P(x,y),B(2,0),由|PB|=3,及椭圆的方程列出方程组即可解出点P的坐标.
解答:解:(1)由题意知曲线C是以A、B为焦点且长轴长为8的椭圆 (3分)
又2c=4,则c=2,a=4,故
 (5分)
(5分)所以曲线C的方程是
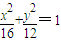 (6分)
(6分)(2)由于A、B两岛收到鱼群发射信号的时间比为5:3,
因此设此时距A、B两岛的距离分别比为5:3(7分)
即鱼群分别距A、B两岛的距离为5海里和3海里. (8分)
设P(x,y),B(2,0),由|PB|=3,
∴
 ,(10分)∴
,(10分)∴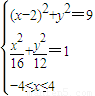 ,(12分)
,(12分)∴x=2,y=±3(13分).
∴点P的坐标为(2,3)或(2,-3)(14分).
点评:本题考查椭圆问题在生产实际中的具体应用,涉及到椭圆方程的求法,椭圆的简单性质,椭圆的直线方程的关系,解题时要认真审题,注意转化思想的灵活运用.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 (2013•奉贤区一模)某海域有A、B两个岛屿,B岛在A岛正东4海里处.经多年观察研究发现,某种鱼群洄游的路线是曲线C,曾有渔船在距A岛、B岛距离和为8海里处发现过鱼群.以A、B所在直线为x轴,AB的垂直平分线为y轴建立平面直角坐标系.
(2013•奉贤区一模)某海域有A、B两个岛屿,B岛在A岛正东4海里处.经多年观察研究发现,某种鱼群洄游的路线是曲线C,曾有渔船在距A岛、B岛距离和为8海里处发现过鱼群.以A、B所在直线为x轴,AB的垂直平分线为y轴建立平面直角坐标系.