题目内容
设函数 满足
满足 ,且对任意
,且对任意 ,都有
,都有
 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若数列 满足:
满足: (
( ),且
),且 ,
求数列
,
求数列 的通项;
的通项;
(Ⅲ)求证: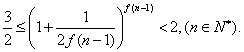
【答案】
解析:(Ⅰ)因 .
若令
.
若令 得
得
再令 得
得 Þ
Þ 
(Ⅱ)∵ ,∴
,∴ ,
,
∴ 又
又 ∴数列
∴数列 是首项为2,公比为3的等比数列,
是首项为2,公比为3的等比数列,
∴
 ,即
,即
(Ⅲ)∵ ,∴T=
,∴T=
 …
…
另一方面:因为 ,
,
所以
综上可得命题成立.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目


