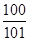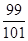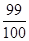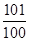题目内容
已知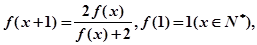 猜想
猜想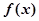 的表达式为( )
的表达式为( )
A.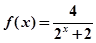 | B.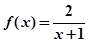 |
C.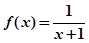 | D.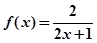 |
B
解析试题分析:∵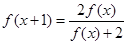 ,
,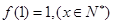 ,∴
,∴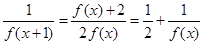 .
.
∴数列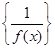 是以
是以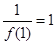 为首项,
为首项,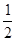 为公差的等差数列.∴
为公差的等差数列.∴ ,
,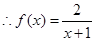 .
.
考点:本题主要考查抽象函数求解析式,进而转化为数列研究数列的通项,考查灵活应用知识分析解决问题的能力和运算能力,知识的迁移能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若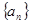 为等差数列,
为等差数列,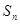 是其前
是其前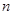 项和,且
项和,且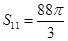 ,则
,则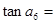 ( )
( )
A.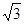 | B.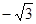 | C. | D.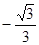 |
已知等差数列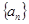 的前
的前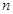 项和是
项和是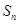 ,若
,若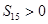 ,
,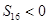 ,则
,则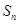 最大值是( )
最大值是( )
A.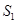 | B.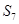 | C.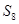 | D.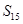 |
设等差数列 的前
的前 项和为
项和为 ,若
,若 ,则
,则 的值是( )
的值是( )
A. | B. | C. | D. |
首项为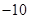 的等差数列,从第
的等差数列,从第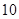 项起开始为正数,则公差
项起开始为正数,则公差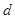 的取值范围是( ).
的取值范围是( ).
A. | B.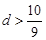 | C.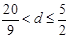 | D.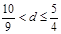 |
等差数列 ,
,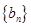 的前
的前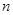 项和分别为
项和分别为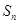 ,
,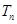 ,若
,若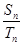 =
=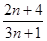 ,则
,则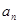 =
=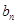 时
时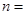 ( )
( )
| A.2 | B.6 | C.无解 | D.无数多个 |
设数列{an}是等差数列,若a3+a4+a5=12,则a1+a2+…+a7=( )
| A.14 | B.21 | C.28 | D.35 |
等差数列{an}的前n项和为Sn,已知S10=0,S15 =25,则nSn的最小值为 ( )
| A.-48 |
| B.-40 |
| C.-49 |
| D.-43 |
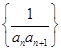 的前100项和为( )
的前100项和为( )