题目内容
已知点 是抛物线
是抛物线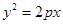
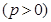 上一点,
上一点,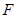 为抛物线的焦点,准线
为抛物线的焦点,准线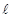 与
与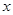 轴交于点
轴交于点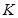 ,已知
,已知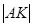 =
=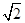
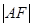 ,三角形
,三角形 的面积等于8.
的面积等于8.
(1)求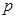 的值;
的值;
(2)过该抛物线的焦点作两条互相垂直的直线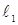 ,
,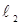 ,与抛物线相交得两条弦,两条弦的中点分别为
,与抛物线相交得两条弦,两条弦的中点分别为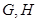 .求
.求 的最小值.
的最小值.
【答案】
(1)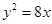 (2)
(2) 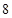
【解析】
试题分析:(1)设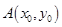 ,因为抛物线的焦点
,因为抛物线的焦点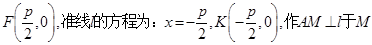 ,
,
则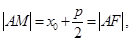 ……1分
……1分
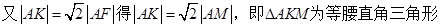 ,
……2分
,
……2分
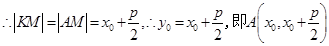 ,而点
,而点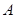 在抛物线上,
在抛物线上,
 ……4分
……4分
又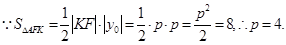
故所求抛物线的方程为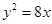 .
……6分
.
……6分
(2)由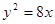 ,得
,得 ,显然直线
,显然直线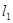 ,
,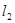 的斜率都存在且都不为0.
的斜率都存在且都不为0.
设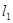 的方程为
的方程为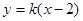 ,则
,则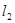 的方程为
的方程为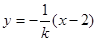 .
.
由 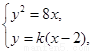 得
得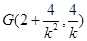 ,同理可得
,同理可得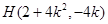 .
……8分
.
……8分
则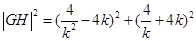
=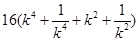
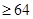 .(当且仅当
.(当且仅当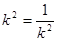 时取等号)
时取等号)
所以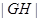 的最小值是
的最小值是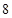 .
……14分
.
……14分
考点:本小题主要考查抛物线标准方程的求解、直线与圆锥曲线的位置关系和利用基本不等式求最值,考查学生分析问题、解决问题的能力和运算求解能力.
点评:设直线方程时,要考虑直线的斜率是否存在;利用基本不等式求最值时,要注意一正二定三相等三个条件缺一不可.

练习册系列答案
相关题目
 是表面积为
是表面积为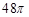 的球面
的球面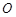 (
(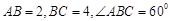 ,则三棱锥
,则三棱锥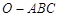 的体积为
的体积为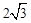 ;②二项式
;②二项式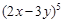 的展开式的各项的系数和为
的展开式的各项的系数和为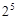 ;③已知函数
;③已知函数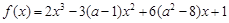 在
在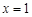 处取得极值,则实数
处取得极值,则实数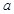 的值是
的值是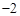 或
或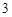 ;④已知点
;④已知点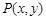 是抛物线
是抛物线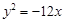 的准线与双曲线
的准线与双曲线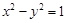 的两条渐近线所围成的三角形区域(含边界)内的任意一点,则
的两条渐近线所围成的三角形区域(含边界)内的任意一点,则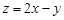 的最大值为9。其中正确命题的序号有__________
的最大值为9。其中正确命题的序号有__________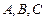 是表面积为
是表面积为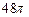 的球面
的球面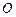 (
(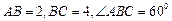 ,则三棱锥
,则三棱锥 的体积为
的体积为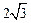 ;②二项式
;②二项式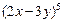 的展开式的各项的系数和为
的展开式的各项的系数和为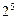 ;③已知函数
;③已知函数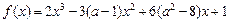 在
在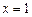 处取得极值,则实数
处取得极值,则实数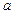 的值是
的值是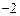 或
或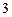 ;④已知点
;④已知点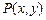 是抛物线
是抛物线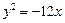 的准线与双曲线
的准线与双曲线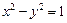 的两条渐近线所围成的三角形区域(含边界)内的任意一点,则
的两条渐近线所围成的三角形区域(含边界)内的任意一点,则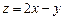 的最大值为9。其中正确命题的序号有__________
的最大值为9。其中正确命题的序号有__________