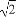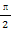题目内容
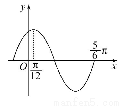
已知f(x)=Asin(ωx+φ)(A>0,ω>0)的最小正周期为2,且当x= 时,f(x)的最大值为2.
时,f(x)的最大值为2.
(1)求f(x)的解析式.
(2)在闭区间[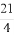 ,
,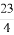 ]上是否存在f(x)的对称轴?如果存在求出其对称轴.若不存在,请说明理由.
]上是否存在f(x)的对称轴?如果存在求出其对称轴.若不存在,请说明理由.
(1) f(x)=2sin(πx+ ) (2) 存在f(x)的对称轴,其方程为x=
) (2) 存在f(x)的对称轴,其方程为x=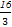 .
.
【解析】(1)由T=2知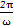 =2得ω=π.
=2得ω=π.
又因为当x=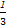 时f(x)max=2知A=2.
时f(x)max=2知A=2.
且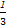 π+φ=2kπ+
π+φ=2kπ+ (k∈Z),
(k∈Z),
故φ=2kπ+ (k∈Z).
(k∈Z).
∴f(x)=2sin(πx+2kπ+ )=2sin(πx+
)=2sin(πx+ ),
),
故f(x)=2sin(πx+ ).
).
(2)令πx+ =kπ+
=kπ+ (k∈Z),
(k∈Z),
得x=k+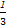 (k∈Z).由
(k∈Z).由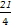 ≤k+
≤k+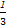 ≤
≤ .
.
得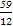 ≤k≤
≤k≤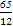 ,又k∈Z,知k=5.
,又k∈Z,知k=5.
故在[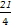 ,
, ]上存在f(x)的对称轴,其方程为x=
]上存在f(x)的对称轴,其方程为x=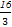 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目