题目内容
设函数f(x)在定义域(0，＋∞)上是单调减函数，且满足f(
)＝1，f(xy)＝f(x)＋f(y)对任意x，y∈(0，＋∞)都成立．求：
(1)f(1)的值；
(2)若f(2＋x)＋f(2－x)＜2，求x的取值范围．
答案：
解析：
解析：
|
(1)令x＝ (2)∵f( ∵函数f(x)在定义域(0，＋∞)上是单调减函数，∴ 由此可以解得x的取值范围是( |
，y＝1，得f(
)＝2，∴f(2＋x)＋f(2－x)＜f(
)．
练习册系列答案
相关题目
,则( )
且a≠-1 B.-1＜a＜0 C.a＜-1或a＞0 D.-1＜a＜2
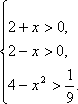
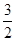)与b=f(
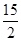)的大小关系为____________.