题目内容
若0<a<2,0<b<2,0<c<2,求证:(2-a)b,(2-b)c,(2-c)a不能同时大于1.
证明:假设(2-a)b,(2-b)c(2-c)a同时大于1.即(2-a)b>1,(2-b)c>1(2-c)a>1,
则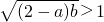 ,
,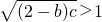 ,
,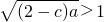 ,
,
所以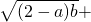
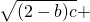
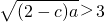 ①.
①.
再由 0<a<2,0<b<2,0<c<2,
可得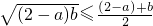 ,
,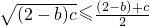 ,
,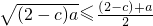 ,
,
故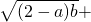
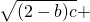
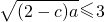 ,这与①矛盾,
,这与①矛盾,
所以假设不成立,即原命题成立.
分析:假设(2-a)b,(2-b)c(2-c)a同时大于1,推出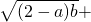
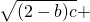
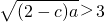 ①;再由已知条件可推出
①;再由已知条件可推出
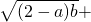
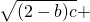
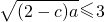 ,这与①矛盾,故假设不成立.
,这与①矛盾,故假设不成立.
点评:本题考查用反证法证明数学命题,把要证的结论进行否定,在此基础上推出矛盾,是解题的关键.
则
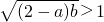 ,
,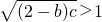 ,
,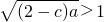 ,
,所以
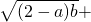
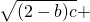
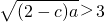 ①.
①.再由 0<a<2,0<b<2,0<c<2,
可得
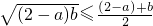 ,
,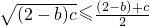 ,
,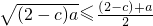 ,
,故
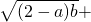
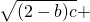
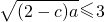 ,这与①矛盾,
,这与①矛盾,所以假设不成立,即原命题成立.
分析:假设(2-a)b,(2-b)c(2-c)a同时大于1,推出
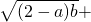
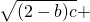
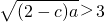 ①;再由已知条件可推出
①;再由已知条件可推出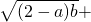
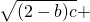
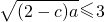 ,这与①矛盾,故假设不成立.
,这与①矛盾,故假设不成立.点评:本题考查用反证法证明数学命题,把要证的结论进行否定,在此基础上推出矛盾,是解题的关键.

练习册系列答案
相关题目