题目内容
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.分别求出函数f(x)和g(x)的解析式.

【答案】分析:根据题意先设出函数解析式,再由图象把点的坐标代入,解方程组即可
解答:解:由题图1得,二次函数f(x)的顶点坐标为(1,2),故可设函数f(x)=a(x-1)2+2(a≠0)
又函数f(x)的图象过点(0,0)
∴a+2=0
∴a=-2
∴f(x)=-2(x-1)2+2
由题图2得,函数g(x)=loga(x+b)的图象过点(0,0)和(1,1),
故有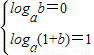 ,解得
,解得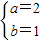
∴g(x)=log2(x+1)
点评:本题考查函数解析式的求法(待定系数法)以及二次函数与对数函数的图象与性质.设二次函数解析式时,需根据条件选择较为简单的形式.属简单题
解答:解:由题图1得,二次函数f(x)的顶点坐标为(1,2),故可设函数f(x)=a(x-1)2+2(a≠0)
又函数f(x)的图象过点(0,0)
∴a+2=0
∴a=-2
∴f(x)=-2(x-1)2+2
由题图2得,函数g(x)=loga(x+b)的图象过点(0,0)和(1,1),
故有
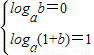 ,解得
,解得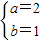
∴g(x)=log2(x+1)
点评:本题考查函数解析式的求法(待定系数法)以及二次函数与对数函数的图象与性质.设二次函数解析式时,需根据条件选择较为简单的形式.属简单题

练习册系列答案
相关题目

 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.分别求出函数f(x)和g(x)的解析式.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.分别求出函数f(x)和g(x)的解析式. (2011•南通模拟)
(2011•南通模拟)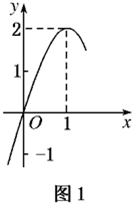 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.