题目内容
、(本小题满分14分)
设函数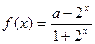 ,其中实常数
,其中实常数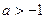 。
。
(1)求函数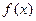 的定义域和值域;
的定义域和值域;
(2)试探究函数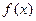 的奇偶性与单调性,并证明你的结论。
的奇偶性与单调性,并证明你的结论。
设函数
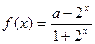 ,其中实常数
,其中实常数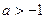 。
。(1)求函数
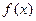 的定义域和值域;
的定义域和值域;(2)试探究函数
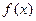 的奇偶性与单调性,并证明你的结论。
的奇偶性与单调性,并证明你的结论。解:(1)函数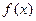 的定义域为
的定义域为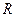 … 2分
… 2分
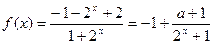 ,当
,当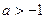 时,因为
时,因为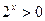 ,所以
,所以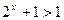 ,
,
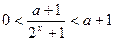 ,从而
,从而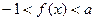 ,所以函数
,所以函数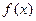 的值域为
的值域为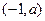 … 6分
… 6分
(2)假设函数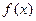 是奇函数,则对于任意的
是奇函数,则对于任意的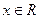 ,有
,有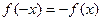 成立,
成立,
即: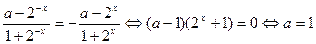
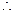 当
当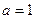 时,函数
时,函数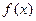 是奇函数.当
是奇函数.当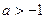 ,且
,且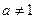 时,函数
时,函数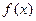 是非奇非偶函数. … 10分
是非奇非偶函数. … 10分
又 对于任意的
对于任意的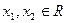 ,且
,且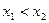 时,
时,
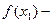
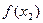
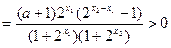
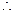 当
当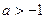 时,函数
时,函数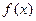 是
是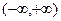 上的单调递减函数. … 14分
上的单调递减函数. … 14分
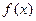 的定义域为
的定义域为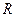 … 2分
… 2分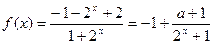 ,当
,当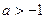 时,因为
时,因为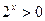 ,所以
,所以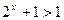 ,
,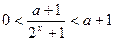 ,从而
,从而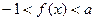 ,所以函数
,所以函数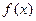 的值域为
的值域为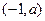 … 6分
… 6分(2)假设函数
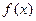 是奇函数,则对于任意的
是奇函数,则对于任意的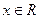 ,有
,有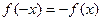 成立,
成立,即:
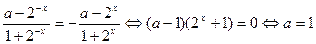
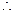 当
当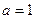 时,函数
时,函数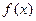 是奇函数.当
是奇函数.当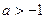 ,且
,且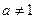 时,函数
时,函数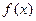 是非奇非偶函数. … 10分
是非奇非偶函数. … 10分又
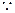 对于任意的
对于任意的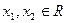 ,且
,且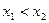 时,
时,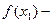
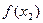
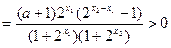
 当
当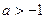 时,函数
时,函数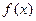 是
是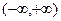 上的单调递减函数. … 14分
上的单调递减函数. … 14分略

练习册系列答案
相关题目
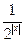 .
.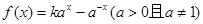 在
在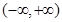 上的单调递增的奇函数,则
上的单调递增的奇函数,则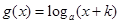 图像是
图像是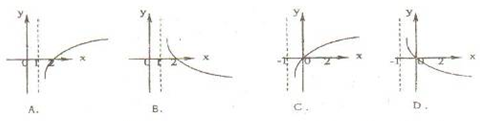
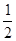 )
)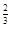 <(
<(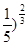 <(
<(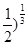 B (
B (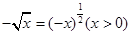
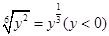
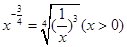
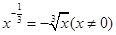
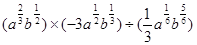 的结果为( )
的结果为( ) 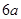
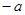
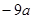
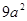
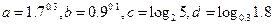 ,那么它们的大小关系是( )
,那么它们的大小关系是( )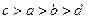
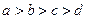
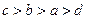
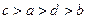
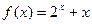 ,
,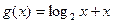 ,
,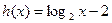 的零点依次为
的零点依次为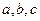 ,则
,则 小关系
小关系 是 ______
是 ______ 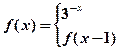
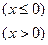 ,若
,若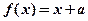 有且仅有三个解,则实数
有且仅有三个解,则实数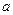 的取值范围是( )
的取值范围是( ) 


