题目内容
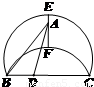
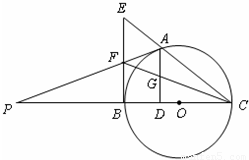
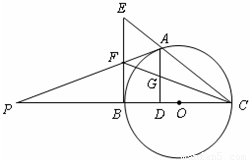
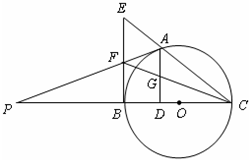
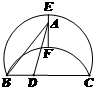 如图E、F是以线段BC为公共弦的两条圆弧的中点,BC=6.点A、D分别为线段EF、BC上的动点.连接AB、AD,设BD=x,AB2-AD2=y,下列图象中,能表示y与x的函数关系的图象是( )
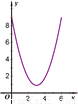
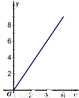
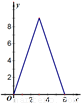
如图E、F是以线段BC为公共弦的两条圆弧的中点,BC=6.点A、D分别为线段EF、BC上的动点.连接AB、AD,设BD=x,AB2-AD2=y,下列图象中,能表示y与x的函数关系的图象是( )A、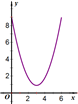 | B、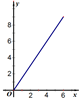 | C、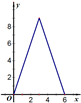 | D、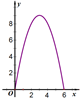 |
分析:由图形及题设条件中的数据知,可延长EF交BC于O,则AB2=BO2+AO2,AD2=AO2+DO2,两者作差即可得到y关于x的解析式,由解析式的类型选择出函数的图象即可
解答:解:由题意如图可延长EF交BC于O,E、F是以线段BC为公共弦的两条圆弧的中点故O是BC中点
AB2=BO2+AO2,AD2=AO2+DO2,
故y=AB2-AD2=BO2-DO2,
又BD=x,BC=6,当D在BO上时,DO=3-x;当D在OC上时DO=x-3
故有y=BO2-DO2=
,即y=6x-x2,0<x≤6
故选D
AB2=BO2+AO2,AD2=AO2+DO2,
故y=AB2-AD2=BO2-DO2,
又BD=x,BC=6,当D在BO上时,DO=3-x;当D在OC上时DO=x-3
故有y=BO2-DO2=
|
故选D
点评:本题考查函数的图象,解答本题关键是根据所给的题设条件建立起函数关系式,由于所得的函数解析式是一个二次函数的形式,由二次函数的性质选出函数的图象.

练习册系列答案
相关题目
 选修4-1:
选修4-1: