题目内容
如右图所示,在三棱锥A-BCD中,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)求证:四边形EFGH是平行四边形;
(2)若AC=BD,求证:四边形EFGH是菱形;
(3)当AC与BD满足什么条件时,四边形EFGH是正方形
【答案】
(1)证明:在△ABC中,E,F分别是边AB,BC中点,所以EF∥AC,且EF=AC,同理有GH∥AC,且GH=AC,
∴EF∥GH且EF=GH,故四边形EFGH是平行四边形;
(2)证明:仿(1)中分析,EH∥BD且EH=BD,若AC=BD,则有EH=EF,又因为四边形EFGH是平行四边形,
∴四边形EFGH是菱形.
(3)由(2)知,AC=BD(四边形EFGH是菱形,欲使EFGH是正方形,还要得到∠EFG=90°,而∠EFG与异面直线AC,BD所成的角有关,故还要加上条件AC⊥BD.∴当AC=BD且AC⊥BD时,四边形EFGH是正方形.
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
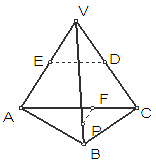 如右图所示,正三棱锥
如右图所示,正三棱锥 (顶点在底面的射影是底面正三角形的中心)中,
(顶点在底面的射影是底面正三角形的中心)中,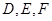 分别是
分别是
 的中点,
的中点,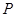 为
为 上任意一点,则直线
上任意一点,则直线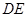 与
与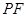 所成的角的大小是( )
所成的角的大小是( )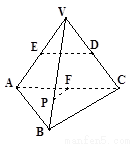
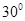 B.
B.  C.
C.  D.随
D.随 (顶点在底面的射影是底面正三角形的中心)中,
(顶点在底面的射影是底面正三角形的中心)中, 分别是
分别是
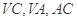 的中点,
的中点,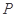 为
为 上任意一点,则直线
上任意一点,则直线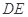 与
与 所成的角的大小是( )
所成的角的大小是( )
 如右图所示,在三棱锥
如右图所示,在三棱锥