题目内容
已知函数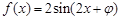 ,其中角
,其中角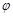 的终边经过点
的终边经过点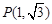 ,且
,且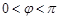 .
.
(1)求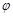 的值;
的值;
(2)求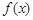 在
在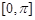 上的单调减区间.
上的单调减区间.
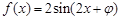 ,其中角
,其中角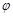 的终边经过点
的终边经过点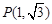 ,且
,且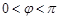 .
.(1)求
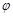 的值;
的值;(2)求
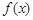 在
在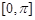 上的单调减区间.
上的单调减区间.(1)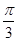 (2)
(2)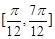
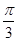 (2)
(2)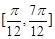
试题分析:(1)这是由角的终边上点的坐标求角的大小的问题,可以通过作图用平面几何知识解决,也可由三角函数的定义,先求出这个角的某个三角函数值,再由角的终边所在的象限和角的范围去确定角的大小;(2)这是一个求函数
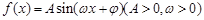 的单调区间的问题,从复合函数的角度出发可知解不等式
的单调区间的问题,从复合函数的角度出发可知解不等式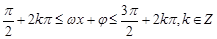 可得到函数的单调递减区间,再和区间
可得到函数的单调递减区间,再和区间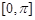 取交集即可.
取交集即可.试题解析:(1)
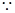 角
角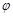 的终边经过点
的终边经过点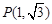 ,
,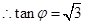 , 4分
, 4分又
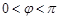 ,
, ; 7分
; 7分(2)因为
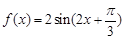 ,由
,由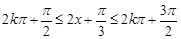 ,
,得
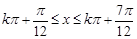 ,
,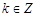 , 11分
, 11分取
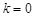 ,则
,则 ,
,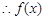 在
在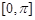 上的单调减区间为
上的单调减区间为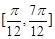 . 14分
. 14分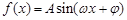 的单调性.
的单调性.
练习册系列答案
相关题目
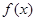 是定义在区间
是定义在区间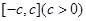 上的奇函数,令
上的奇函数,令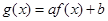 ,并有关于函数
,并有关于函数 的四个论断:
的四个论断: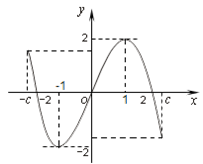
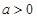 ,对于
,对于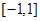 内的任意实数
内的任意实数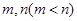 ,
,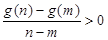 恒成立;
恒成立;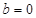 ;
;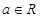 ,
,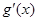 有两个零点;
有两个零点;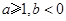 ,则方程
,则方程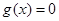 必有3个实数根;
必有3个实数根; ,若有四个不同的正数
,若有四个不同的正数 满足
满足 (
( 为常数),且
为常数),且 ,
, ,则
,则 的值为( )
的值为( )

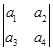 =a1a4-a2a3;将函数f(x)=
=a1a4-a2a3;将函数f(x)=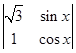 的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为( )
的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为( )
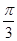
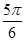

 ,函数
,函数 图像向右平移
图像向右平移 个单位与原图像重合,则
个单位与原图像重合,则 最小值是( )
最小值是( )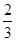


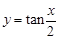 的图象的对称中心是
的图象的对称中心是 ;
; 在
在 上连续,
上连续, ;
; 的图象可由函数
的图象可由函数 的图象向右平移
的图象向右平移 个单位得到;
个单位得到; 上的导数
上的导数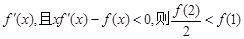 ;
; 的递减区间是
的递减区间是
 .
. 的图像向右平移
的图像向右平移 个单位后与原函数的图像关于
个单位后与原函数的图像关于 轴对称,则
轴对称,则 的最小正值是 ( )
的最小正值是 ( )
 ,函数
,函数 在
在 上单调递减,则
上单调递减,则 的取值范围是( )
的取值范围是( )


