题目内容
已知函数 。
。
(1)讨论函数 在定义域内的最值(4分);
在定义域内的最值(4分);
(2)已知数列 满足
满足 。
。
① 证明对一切 且
且 ,
, (4分);
(4分);
② 证明对一切 ,
, (这里
(这里 是自然对数的底数)(6分)。
是自然对数的底数)(6分)。
【答案】
(1)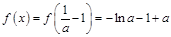 为
为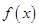 在定义域内的最大值;
在定义域内的最大值;
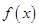 在其定义域
在其定义域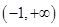 内无最小值
内无最小值
(2)证明略
【解析】(1)当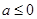 时,
时,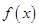 在其定义域
在其定义域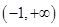 内是增函数,无最值;………1分
内是增函数,无最值;………1分
当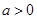 时,
时, ,由
,由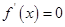 ,
,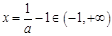 ,
,
且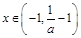 时,
时,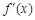 >0,
>0,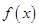 在
在 内递增;
内递增;
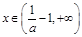 时,
时,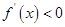 ,
,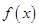 在
在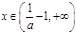 内递减,
内递减,
故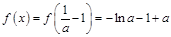 为
为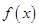 在定义域内的最大值;
在定义域内的最大值;
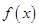 在其定义域
在其定义域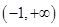 内无最小值
…………………4分
内无最小值
…………………4分
(2)① 易用数学归纳法证明。 …………………8分
②
当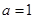 时,由第(1)小题知
时,由第(1)小题知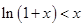 对
对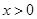 恒成立,
恒成立,
由① 知 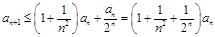
所以

所以
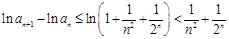 。
。
显然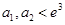 ;因为
;因为 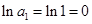 ,所以
,所以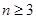 时,
时,
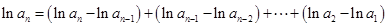
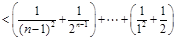
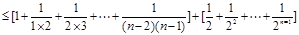
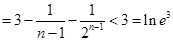 ,
,
所以
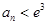 ,综合知对一切
,综合知对一切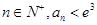 。 …………………14分
。 …………………14分

练习册系列答案
相关题目
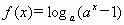 ,(
,(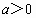 ,
,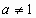 ),
),
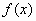 的定义域;
的定义域;
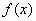 的单调性.
的单调性.