题目内容
已知函数 (a,b,c∈N),且f(2)=2,f(3)<3,
(a,b,c∈N),且f(2)=2,f(3)<3,且f(x)的图象按向量
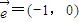 平移后得到的图象关于原点对称.
平移后得到的图象关于原点对称.(1)求a、b、c的值;
(2)设0<|x|<1,0<|t|≤1,求证不等式|t+x|-|t-x|<|f(tx+1)|;
(3)已知x>0,n∈N*,求证不等式[f(x+1)]n-f(xn+1)≥2n-2.
【答案】分析:(1)由f(x)的图象按向量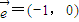 平移后得到的图象关于原点对称,可以求出c的值;根据f(2)=2,f(3)<3,
平移后得到的图象关于原点对称,可以求出c的值;根据f(2)=2,f(3)<3,
可以求出a、b的值;
(2)利用绝对值不等式的性质,证明左边大于等于2,右边小于2即可;
(3)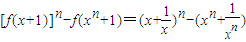 ,再借助于二项式的系数的性质可证.
,再借助于二项式的系数的性质可证.
解答:解:(1)将f(x)的图象按向量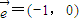 平移后得到的解析式为
平移后得到的解析式为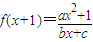
若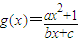 关于原点对称,则当x=0时有意义,必有g(0)=0…(2分)
关于原点对称,则当x=0时有意义,必有g(0)=0…(2分)
而g(0)≠0,所以c=0,且b≠0
∵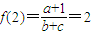 ,∴
,∴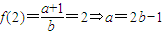 ,
,
∵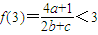 ,∴
,∴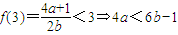
∴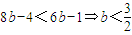 ,
,
又b∈N,b≠0,所以b=1,a=1∴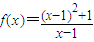 …(4分)
…(4分)
(2)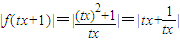
∵tx与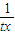 同号,所以
同号,所以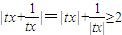 …(6分)
…(6分)
而|t+x|-|t-x|≤|t+x-(t-x)|=2|x|<2
∴|t+x|-|t-x|<|f(tx+1)|…(8分)
(3)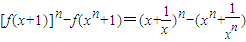 …(9分)
…(9分)
令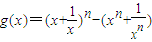 ,(x>0)
,(x>0)
则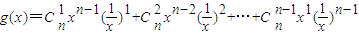 ,…..①
,…..①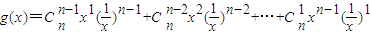 …..②
…..②
①②相加得
=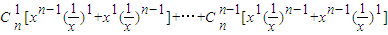 …(12分)
…(12分)
≥2(Cn1+Cn2+…+Cnn-1)=2(2n-2)
∴g(x)≥2n-2,即[f(x+1)]n-f(xn+1)≥2n-2,当x=1时取等号…(14分)
点评:本题主要考查函数解析式的求解,考查绝对值不等式的性质,综合性强.
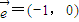 平移后得到的图象关于原点对称,可以求出c的值;根据f(2)=2,f(3)<3,
平移后得到的图象关于原点对称,可以求出c的值;根据f(2)=2,f(3)<3,可以求出a、b的值;
(2)利用绝对值不等式的性质,证明左边大于等于2,右边小于2即可;
(3)
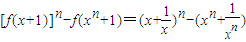 ,再借助于二项式的系数的性质可证.
,再借助于二项式的系数的性质可证.解答:解:(1)将f(x)的图象按向量
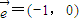 平移后得到的解析式为
平移后得到的解析式为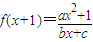
若
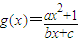 关于原点对称,则当x=0时有意义,必有g(0)=0…(2分)
关于原点对称,则当x=0时有意义,必有g(0)=0…(2分)而g(0)≠0,所以c=0,且b≠0
∵
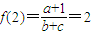 ,∴
,∴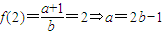 ,
,∵
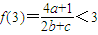 ,∴
,∴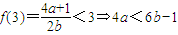
∴
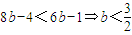 ,
,又b∈N,b≠0,所以b=1,a=1∴
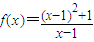 …(4分)
…(4分)(2)
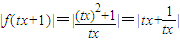
∵tx与
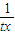 同号,所以
同号,所以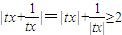 …(6分)
…(6分)而|t+x|-|t-x|≤|t+x-(t-x)|=2|x|<2
∴|t+x|-|t-x|<|f(tx+1)|…(8分)
(3)
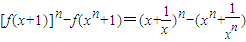 …(9分)
…(9分)令
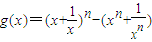 ,(x>0)
,(x>0)则
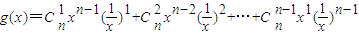 ,…..①
,…..①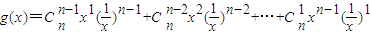 …..②
…..②①②相加得

=
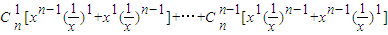 …(12分)
…(12分)≥2(Cn1+Cn2+…+Cnn-1)=2(2n-2)
∴g(x)≥2n-2,即[f(x+1)]n-f(xn+1)≥2n-2,当x=1时取等号…(14分)
点评:本题主要考查函数解析式的求解,考查绝对值不等式的性质,综合性强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
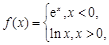 则
则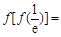 ( )
( )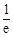 B.
B.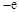 C.
C.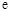 D.
D.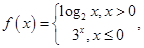 则
则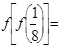 ( )
( )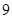 B.
B.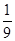 C.
C.
 D.
D.
 已知函数
已知函数  若
若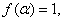
 =
=