题目内容
手表的表面在一平面上.整点1,2,…,12这12个数字等间隔地分布在半径为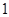 的圆周上.从整点
的圆周上.从整点 到整点
到整点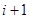 的向量记作
的向量记作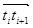 ,则
,则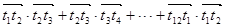 = .
= .
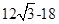
解析试题分析:因为整点把圆分成12份,所以每一份所对应的圆心角是30度,连接相邻的两点与圆心组成等腰三角形底边平方为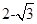 ,每对向量的夹角为30°,所以每对向量的数量积为
,每对向量的夹角为30°,所以每对向量的数量积为 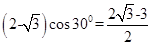 ,
,
所以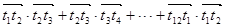 =
=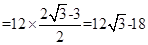 。
。
考点:平面向量的数量积运算;数列求和。
点评:本题是向量数量积的运算,条件中没有直接给出两个向量的模和两向量的夹角,只是题目所用的向量要应用圆的性质来运算,把向量的数量积同解析几何问题结合在一起,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
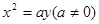 的准线方程是 ____________.
的准线方程是 ____________.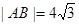 ,则双曲线C的方程为__________.
,则双曲线C的方程为__________.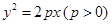 的焦点与双曲线
的焦点与双曲线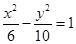 的右焦点重合,则实数
的右焦点重合,则实数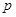 的值是 .
的值是 .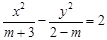 表示焦点在x轴上的双曲线,则m的取值范围是 .
表示焦点在x轴上的双曲线,则m的取值范围是 .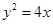 的焦点,且被圆
的焦点,且被圆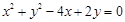 截得弦最长的直线的方程是 。
截得弦最长的直线的方程是 。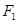 、
、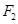 是椭圆
是椭圆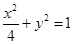 的左、右焦点,弦
的左、右焦点,弦 过
过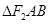 的周长为 .
的周长为 .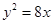 的焦点坐标是 .
的焦点坐标是 .