题目内容
设矩形的长为a,宽为b,其比满足b:a=
≈0.618,这种矩形给人以美感称为黄金矩形.黄金矩形常应用于工艺品设计中.下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是( )
| ||
| 2 |
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是( )
| A、甲批次的总体平均数与标准值更接近 |
| B、乙批次的总体平均数与标准值更接近 |
| C、两个批次总体平均数与标准值接近程度相同 |
| D、两个批次总体平均数与标准值接近程度不能确定 |
分析:本题考查的知识点是平均数,要计算哪个批次的总体平均数与标准值更接近,我们可分别抽取两个批次的初加工矩形宽度与长度的比值样本:甲批次:0.598 0.625 0.628 0.595 0.639与乙批次:0.618 0.613 0.592 0.622 0.620,分别代入平均数计算公式,计算出平均数后,再与标准值0.618比较,越接近说明总体平均数与标准值更接近.
解答:解:甲批次的平均数为0.617,
乙批次的平均数为0.613.
故甲批次的总体平均数与标准值更接近
故选A.
乙批次的平均数为0.613.
故甲批次的总体平均数与标准值更接近
故选A.
点评:平均数反映的是数据的总体平均水平,其值越大,则其总体平均水平越高;其值越小,则其总体平均水平越低;其值与标准值之间的差越小,则其总体平均水平与标准越接近.

练习册系列答案
相关题目
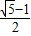 ≈0.618,这种矩形给人以美感称为黄金矩形.黄金矩形常应用于工艺品设计中.下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
≈0.618,这种矩形给人以美感称为黄金矩形.黄金矩形常应用于工艺品设计中.下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本: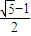 ≈0.618,这种矩形给人以美感称为黄金矩形.黄金矩形常应用于工艺品设计中.下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
≈0.618,这种矩形给人以美感称为黄金矩形.黄金矩形常应用于工艺品设计中.下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本: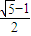 ≈0.618,这种矩形给人以美感称为黄金矩形.黄金矩形常应用于工艺品设计中.下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
≈0.618,这种矩形给人以美感称为黄金矩形.黄金矩形常应用于工艺品设计中.下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本: