题目内容
已知集合{x|x2+(k+2)x+1=0,x∈R}∩R+= ,则实数k的取值范围是( )
,则实数k的取值范围是( )
| A.-4<k<0 | B.k>-4 | C.k>-2 | D.k≥0 |
B
解析试题分析:设A={x|x2+(k+2)x+1=0,x∈R},由A∩R+= ,得当A=
,得当A= 时,
时,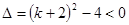 ,解得,-4<k<0;当
,解得,-4<k<0;当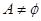 时,方程有两个非正数实根,则
时,方程有两个非正数实根,则 ,解得
,解得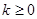 .综上,k>-4.
.综上,k>-4.
故选B.
考点:一元二次方程根的分布,分类讨论思想.

练习册系列答案
相关题目
已知集合 ,
, ,则
,则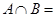 ( ).
( ).
A. | B.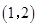 |
C. | D. |
设集合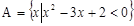 ,
,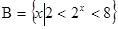 ,则( )
,则( )
A.A B B | B.A B B | C.A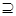 B B | D.A B B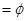 |
设全集 ,集合
,集合 ,
, ,则
,则 ( )
( )
A. | B.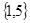 | C.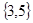 | D. |
已知全集为R,集合M ={xlx2-2x-8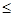 0),集合N={x|l-x<0},则集合M
0),集合N={x|l-x<0},则集合M (CRN)等于( )
(CRN)等于( )
| A.[-2,1] | B.(1,+ ) ) | C.[-l,4) | D.(1,4] |
已知全集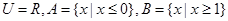 ,则集合
,则集合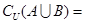 ( )
( )
A.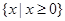 | B.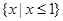 | C.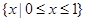 | D.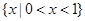 |
 中的元素
中的元素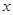 应满足的条件是 .
应满足的条件是 .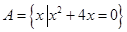
 .
. 求a的值;
求a的值; ,求a的值;
,求a的值;