题目内容
10.已知等比数列{an}的前n项和为Sn=an-1(a>0,且a≠1),且6a1,a3,a2成等差数列.(1)求数列{an}的通项公式;
(2)设bn=$\frac{{a}_{n+1}}{({a}_{n}+1)({a}_{n+1}+1)}$(n∈N*),求数列{bn}的前n项和Tn.
分析 (1)由Sn=an-1(a>0,且a≠1),可得当n=1时,a1=a-1,a2=S2-S1.可得等比数列{an}的公比q=$\frac{{a}_{2}}{{a}_{1}}$.由于6a1,a3,a2成等差数列,可得6a1+a2=2a3,代入即可得出.
(2)bn=$\frac{{2}^{n}}{({2}^{n-1}+1)({2}^{n}+1)}$=$2(\frac{1}{{2}^{n-1}+1}-\frac{1}{{2}^{n}+1})$.利用“裂项求和”即可得出.
解答 解:(1)∵Sn=an-1(a>0,且a≠1),∴当n=1时,a1=a-1,a2=S2-S1=(a2-1)-(a-1)=a(a-1).
∴等比数列{an}的公比q=$\frac{{a}_{2}}{{a}_{1}}$=a.∵6a1,a3,a2成等差数列,∴6a1+a2=2a3,6a1+a1a=$2{a}_{1}{a}^{2}$,化为2a2-a-6=0,a>0,解得a=2.∴an=2n-1.
(2)bn=$\frac{{a}_{n+1}}{({a}_{n}+1)({a}_{n+1}+1)}$=$\frac{{2}^{n}}{({2}^{n-1}+1)({2}^{n}+1)}$=$2(\frac{1}{{2}^{n-1}+1}-\frac{1}{{2}^{n}+1})$.
∴Tn=$2[(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{{2}^{n-1}+1}-\frac{1}{{2}^{n}+1})]$=2$(\frac{1}{2}-\frac{1}{{2}^{n}+1})$=$\frac{{2}^{n}-1}{{2}^{n}+1}$.
点评 本题考查了等差数列与等比数列的通项公式、“裂项求和”、递推关系的应用,考查了推理能力与计算能力,属于中档题.

| A. | -$\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
| A. | $\widehat{y}$=5-17x | B. | $\widehat{y}$=-17+5x | C. | $\widehat{y}$=17+5x | D. | $\widehat{y}$=17-5x |
| A. | 225 | B. | 345 | C. | 350 | D. | 535 |
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
| A. | a≤-4 | B. | a≤-2 | C. | a≥-2 | D. | a>-4 |
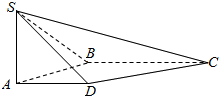 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.