题目内容
已知幂函数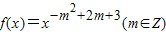 为偶函数且在区间(0,+∞)上是单调增函数.
为偶函数且在区间(0,+∞)上是单调增函数.(1)求函数f(x)的解析式;
(2)设函数
 ,若g(x)>0对任意x∈[-1,1]恒成立,求实数q的取值范围.
,若g(x)>0对任意x∈[-1,1]恒成立,求实数q的取值范围.
【答案】分析:1)由幂函数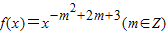 为偶函数且在区间(0,+∞)上是单调增函数,可得-m2+2m+3>0且-m2+2m+3为偶数,解不等式可得结合,m∈Z可求m的取值
为偶函数且在区间(0,+∞)上是单调增函数,可得-m2+2m+3>0且-m2+2m+3为偶数,解不等式可得结合,m∈Z可求m的取值
(2)由(1)可得,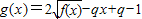 =2x2-qx+q-1>0,q(1-x)>1-2x2,结合-1≤x≤1可得x≠1时q
=2x2-qx+q-1>0,q(1-x)>1-2x2,结合-1≤x≤1可得x≠1时q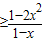 在[-1,1]上恒成立,从而转化为求h(x)=
在[-1,1]上恒成立,从而转化为求h(x)=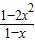 在[-1,1]上的最大值即可
在[-1,1]上的最大值即可
解答:解:(1)由幂函数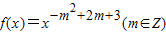 为偶函数且在区间(0,+∞)上是单调增函数
为偶函数且在区间(0,+∞)上是单调增函数
-m2+2m+3>0且-m2+2m+3为偶数
解不等式可得,-1<m<3,m∈Z
∴m=0,1,2
当m=0时,-m2+2m+3=3(舍)
当m=1时,-m2+2m+3=4
当m=2时,-m2+2m+3=3(舍)
故m=1,f(x)=x4
(2)由(1)可得,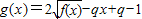 =2x2-qx+q-1>0
=2x2-qx+q-1>0
q(1-x)>1-2x2
-1≤x≤1
x≠1时,q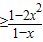 在[-1,1]上恒成立
在[-1,1]上恒成立
令h(x)=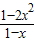 =-[2(1-x)+
=-[2(1-x)+ ]+4≤4-2
]+4≤4-2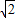
q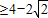
点评:本题主要考查了幂函数的性质可应用,解题的关键是由函数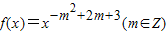 为偶函数且在区间(0,+∞)上是单调增函数,可得-m2+2m+3>0且-m2+2m+3为偶数,而函数的恒成立问题往往转化为求解函数的最值,注意构造函数的应用.
为偶函数且在区间(0,+∞)上是单调增函数,可得-m2+2m+3>0且-m2+2m+3为偶数,而函数的恒成立问题往往转化为求解函数的最值,注意构造函数的应用.
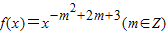 为偶函数且在区间(0,+∞)上是单调增函数,可得-m2+2m+3>0且-m2+2m+3为偶数,解不等式可得结合,m∈Z可求m的取值
为偶函数且在区间(0,+∞)上是单调增函数,可得-m2+2m+3>0且-m2+2m+3为偶数,解不等式可得结合,m∈Z可求m的取值(2)由(1)可得,
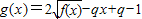 =2x2-qx+q-1>0,q(1-x)>1-2x2,结合-1≤x≤1可得x≠1时q
=2x2-qx+q-1>0,q(1-x)>1-2x2,结合-1≤x≤1可得x≠1时q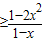 在[-1,1]上恒成立,从而转化为求h(x)=
在[-1,1]上恒成立,从而转化为求h(x)=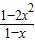 在[-1,1]上的最大值即可
在[-1,1]上的最大值即可解答:解:(1)由幂函数
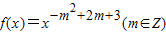 为偶函数且在区间(0,+∞)上是单调增函数
为偶函数且在区间(0,+∞)上是单调增函数-m2+2m+3>0且-m2+2m+3为偶数
解不等式可得,-1<m<3,m∈Z
∴m=0,1,2
当m=0时,-m2+2m+3=3(舍)
当m=1时,-m2+2m+3=4
当m=2时,-m2+2m+3=3(舍)
故m=1,f(x)=x4
(2)由(1)可得,
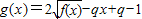 =2x2-qx+q-1>0
=2x2-qx+q-1>0q(1-x)>1-2x2
-1≤x≤1
x≠1时,q
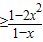 在[-1,1]上恒成立
在[-1,1]上恒成立令h(x)=
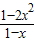 =-[2(1-x)+
=-[2(1-x)+ ]+4≤4-2
]+4≤4-2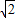
q
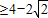
点评:本题主要考查了幂函数的性质可应用,解题的关键是由函数
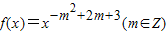 为偶函数且在区间(0,+∞)上是单调增函数,可得-m2+2m+3>0且-m2+2m+3为偶数,而函数的恒成立问题往往转化为求解函数的最值,注意构造函数的应用.
为偶函数且在区间(0,+∞)上是单调增函数,可得-m2+2m+3>0且-m2+2m+3为偶数,而函数的恒成立问题往往转化为求解函数的最值,注意构造函数的应用. 
练习册系列答案
相关题目
 为偶函数且在区间(0,+∞)上是单调递减函数。(1)求函数f(x)的解析式;(2)讨论函数
为偶函数且在区间(0,+∞)上是单调递减函数。(1)求函数f(x)的解析式;(2)讨论函数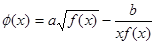 的奇偶性。(10分)
的奇偶性。(10分)  为偶函数且在区间(0,+∞)上是单调增函数.
为偶函数且在区间(0,+∞)上是单调增函数.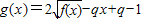 ,若g(x)>0对任意x∈[-1,1]恒成立,求实数q的取值范围.
,若g(x)>0对任意x∈[-1,1]恒成立,求实数q的取值范围.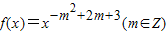 为偶函数且在区间(0,+∞)上是单调增函数.
为偶函数且在区间(0,+∞)上是单调增函数.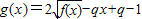 ,若g(x)>0对任意x∈[-1,1]恒成立,求实数q的取值范围.
,若g(x)>0对任意x∈[-1,1]恒成立,求实数q的取值范围.