题目内容
若向量
=（2，-x）与
=（x，-8）共线且方向相反，则x=________．
-4
分析：根据两个向量共线，写出两个向量共线的坐标形式的充要条件（2，-x）=λ（x，-8），根据横标和纵标分别相等，得到关于x，λ的方程组，解出方程组，根据两个向量共线且反向，得到结果．
解答：∵向量=（2，-x）与=（x，-8）共线
∴=λ
∴（2，-x）=λ（x，-8）
∴2=λx，-x=-8λ
∴λ=
∵两个向量共线且方向相反
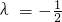
∴x=-4
故答案为：-4．
点评：本题考查平面向量共线的坐标表示，是一个基础题，这种题目可以作为一个解答题目的一部分，也可以作为选择和填空单独出现，是一个送分题目．
分析：根据两个向量共线，写出两个向量共线的坐标形式的充要条件（2，-x）=λ（x，-8），根据横标和纵标分别相等，得到关于x，λ的方程组，解出方程组，根据两个向量共线且反向，得到结果．
解答：∵向量
=（2，-x）与=（x，-8）共线∴
=λ∴（2，-x）=λ（x，-8）
∴2=λx，-x=-8λ
∴λ=
∵两个向量共线且方向相反
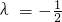
∴x=-4
故答案为：-4．
点评：本题考查平面向量共线的坐标表示，是一个基础题，这种题目可以作为一个解答题目的一部分，也可以作为选择和填空单独出现，是一个送分题目．
练习册系列答案
同步练习强化拓展系列答案
相关题目
已知向量p=（2，x-1），q=（x，-3），且p⊥q，若由x的值构成的集合A满足A?{x|ax=2}，则实数a构成的集合是（ ）
| A、{0} | ||
B、{
| ||
| C、空集 | ||
D、{0，
|
已知向量
=（1，2），
=（x，4），若向量
∥
，则x=（ ）
| a |
| b |
| a |
| b |
| A、2 | B、-2 | C、8 | D、-8 |