题目内容
设 ,函数
,函数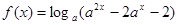 ,则使
,则使 的
的 的取值范围是( )
的取值范围是( )
A. | B.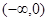 | C. | D. |
C
解析试题分析:结合对数函数、指数函数的性质和复合函数的单调性可知:当0<a<1,loga(a2x-2ax-2)<0时,有a2x-2ax-2>1,解可得答案.
解:设0<a<1,函数f(x)=loga(a2x-2ax-2),
若f(x)<0
则loga(a2x-2ax-2)<0,∴a2x-2ax-2>1
∴(ax-3)(ax+1)>0∴ax-3>0,∴x<loga3,
故选C.
考点:对数函数图象与性质的综合应用;复合函数的单调性

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数 在
在 上为减函数,则
上为减函数,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数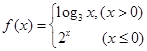 ,则
,则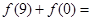 ( )
( )
| A.0 | B.1 | C.2 | D.3 |
函数 在
在 上的图像如图所示(其中e为自然对数底),则
上的图像如图所示(其中e为自然对数底),则 值可能是( )
值可能是( )
A. | B. | C. | D. |
函数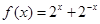 的图象关于 对称. ( )
的图象关于 对称. ( )
| A.坐标原点 | B.直线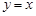 | C. 轴 轴 | D.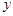 轴 轴 |
设 则 ( )
则 ( )
A. | B. | C. | D. |
已知f(x)的定义域是(0,1),则f[( )x]的定义域为( )
)x]的定义域为( )
| A.(0,1) | B.( ,1) ,1) | C.(-∞,0) | D.(0,+ ∞) |
设 ,则函数
,则函数 ( )
( )
A.在 上单调递减,在 上单调递减,在 上单调递增 上单调递增 |
B.在 上单调递增,在 上单调递增,在 上单调递减 上单调递减 |
C.在 上单调递增,在 上单调递增,在 上单调递增 上单调递增 |
D.在 上单调递减,在 上单调递减,在 上单调递减 上单调递减 |
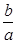 )x的图象只可能是( )
)x的图象只可能是( )