题目内容
已知向量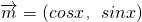 ,
,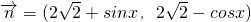 ,函数f(x)=
,函数f(x)= ,x∈R.
,x∈R.
(1)求函数f(x)的最大值;
(2)若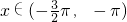 ,且f(x)=1,求
,且f(x)=1,求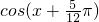 的值.
的值.
解:(1)因为 =
=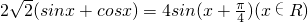
∴f(x)的最大值是4.
(2)∵f(x)=1,∴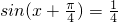 ,
,
又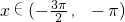 ,即
,即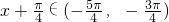 ,
,
所以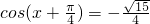 ,
,
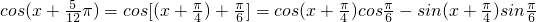
=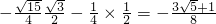 .
.
分析:(1)先由向量的数量积坐标表示得到函数的三角函数解析式,再将其化简得到f(x)=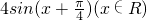 ,最大值易得;
,最大值易得;
(2)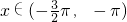 ,且f(x)=1,解三角方程求出符合条件的x的三角函数值,再有余弦的和角公式求
,且f(x)=1,解三角方程求出符合条件的x的三角函数值,再有余弦的和角公式求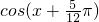 的值
的值
点评:本题考查平面向量的综合题以及三角函数的恒等变换求值,解题的关键是熟练掌握向量的数量积公式及三角恒等变换公式,本题涉及到向量与三角恒等变换,综合性较强,变形灵活,主要考查了变形的能力及利用公式计算求值的能力
 =
=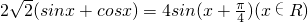
∴f(x)的最大值是4.
(2)∵f(x)=1,∴
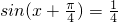 ,
,又
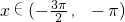 ,即
,即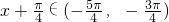 ,
,所以
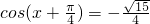 ,
,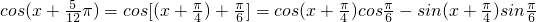
=
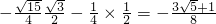 .
.分析:(1)先由向量的数量积坐标表示得到函数的三角函数解析式,再将其化简得到f(x)=
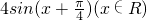 ,最大值易得;
,最大值易得;(2)
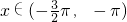 ,且f(x)=1,解三角方程求出符合条件的x的三角函数值,再有余弦的和角公式求
,且f(x)=1,解三角方程求出符合条件的x的三角函数值,再有余弦的和角公式求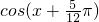 的值
的值点评:本题考查平面向量的综合题以及三角函数的恒等变换求值,解题的关键是熟练掌握向量的数量积公式及三角恒等变换公式,本题涉及到向量与三角恒等变换,综合性较强,变形灵活,主要考查了变形的能力及利用公式计算求值的能力

练习册系列答案
相关题目
 ,
,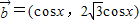 ,函数f(x)=
,函数f(x)=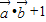 .
.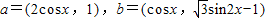 ,设函数f(x)=a•b,其中x∈R.
,设函数f(x)=a•b,其中x∈R.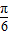 个单位得到g(x)的图象,求g(x)的解析式.
个单位得到g(x)的图象,求g(x)的解析式. ,
,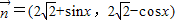 ,函数f(x)=
,函数f(x)= ,x∈R.
,x∈R.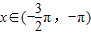 ,且f(x)=1,求
,且f(x)=1,求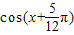 的值.
的值. ,
, ,函数f(x)=
,函数f(x)=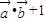 .
. ,
, ,函数f(x)=
,函数f(x)= .
.