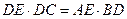题目内容
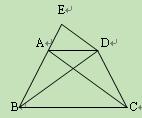
已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.
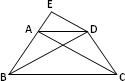
求证:(1)△ABC≌△DCB
(2)DE·DC=AE·BD.
答案:
解析:
解析:
|
证明: (1)∵四边形ABCD是等腰梯形,∴AC=DB
∵AB=DC,BC=CB,∴△ABC≌△BCD (2)∵△ABC≌△BCD,∴∠ACB=∠DBC,∠ABC=∠DCB ∵AD∥BC,∴∠DAC=∠ACB,∠EAD=∠ABC ∵ED∥AC,∴∠EDA=∠DAC ∴∠EDA=∠DBC,∠EAD=∠DCB ∴△ADE∽△CBD ∴DE:BD=AE:CD,∴DE·DC=AE·BD |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

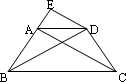
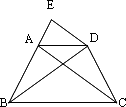
 中,
中, ,过点
,过点 作
作 的平行线
的平行线 ,交
,交 的延长线于点
的延长线于点 .求证:⑴
.求证:⑴  ⑵
⑵ 

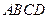 中,
中,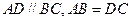 ,过点
,过点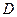 作
作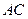 的平行线
的平行线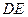 ,交
,交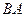 的延长线于点
的延长线于点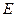 .求证:⑴
.求证:⑴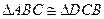 ⑵
⑵