题目内容
“m<2”是“关于x的一元二次方程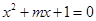
有实数解”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
【答案】
D
【解析】略
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
开心试卷期末冲刺100分系列答案双基同步导航训练系列答案黄冈小状元同步计算天天练系列答案题目内容
“m<2”是“关于x的一元二次方程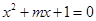有实数解”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
D
【解析】略
开心试卷期末冲刺100分系列答案双基同步导航训练系列答案黄冈小状元同步计算天天练系列答案
已知集合A={x|－2≤x≤7},B={x|m+1<x<2m－1}且B≠
,若A∪B=A，则( )
在（-1，1）内有零点，所以f(-1)f(1)<0,即（2+m）(2-m)<0，则m>2或m<-2
的所有等可能取值为1,2…,n，若
，则（ ）
的两零点分别是1与2，所以
，即
，解得
解析：因为
只有一个零点，所以方程
只有一个根，因此
，所以
，P＝logca，N＝logcb，M＝logc(ab)，则有( )
的图象与x轴有公共点，则m的取值范围是（ ）