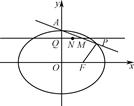
题目内容
如图;已知椭圆C: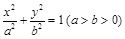 的离心率为
的离心率为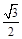 ,以椭圆的左顶点T为圆心作圆T:
,以椭圆的左顶点T为圆心作圆T: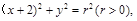 设圆T与椭圆C交于点M、N.
设圆T与椭圆C交于点M、N.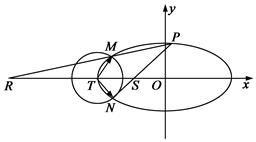
(1)求椭圆C的方程;
(2)求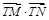 的最小值,并求此时圆T的方程;
的最小值,并求此时圆T的方程;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与 轴交于点R,S,O为坐标原点。求证:
轴交于点R,S,O为坐标原点。求证: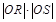 为定值.
为定值.
(1)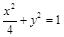 (2)
(2)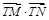 取得最小值为-
取得最小值为- ,圆T的方程为:
,圆T的方程为: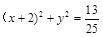 ;
;
(3)
解析试题分析:(1)椭圆C: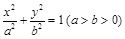 的离心率为
的离心率为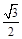


由椭圆的左顶点为 ,所以
,所以
 可得椭圆的标准方程
可得椭圆的标准方程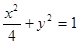 ;
;
(2)点M与点N关于 轴对称,设
轴对称,设 ,
,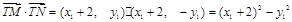
 ,再根据
,再根据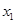 的取值范围求出
的取值范围求出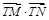 的最小值,并由取得最小值的条件确定
的最小值,并由取得最小值的条件确定 ,进而确定圆
,进而确定圆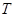 的半径.
的半径.
(3)设点 ,利用点
,利用点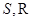 分别是直线
分别是直线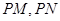 与
与 轴的交点,把
轴的交点,把 用
用 表示,
表示,
而 ,结合点
,结合点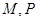 都在椭圆上,将表达式化简即可.
都在椭圆上,将表达式化简即可.
试题解析:
解:(1)由题意知 解之得;
解之得; ,由
,由 得b=1,
得b=1,
故椭圆C方程为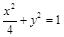 ;3分
;3分
(2)点M与点N关于 轴对称,
轴对称,
设 不妨 设
不妨 设 .
.
由于点M在椭圆C上,
 ,
,
由已知 ,
,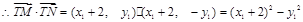 ,
,
阶段 ;
;
由于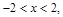 故当
故当 时,
时,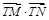 取得最小值为-
取得最小值为- ,
,
当 时
时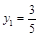 ,故
,故 又点M在圆T上,代入圆的方程得
又点M在圆T上,代入圆的方程得 ,故圆T的方程为:
,故圆T的方程为: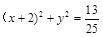 ;...8分
;...8分
(3)设 ,则直线MP的方程为
,则直线MP的方程为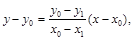
令 ,得
,得 ,同理
,同理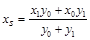 , 故
, 故 ,10分
,10分
又点M与点P在椭圆上,故 ,
,
得 ,
, 为定值..14分
为定值..14分
考点:1、椭圆的标准方程;2、圆的标准方程序;3、向量的数量积;4直线的方程.

练习册系列答案
相关题目
 的离心率是
的离心率是 .
. ,使点C(2,0)关于直线
,使点C(2,0)关于直线 :
: 的离心率为
的离心率为 ,其长轴长与短轴长的和等于6.
,其长轴长与短轴长的和等于6.
 ,
, 是椭圆上异于
是椭圆上异于 分别交
分别交 轴于点
轴于点 ,若直线
,若直线 与过点
与过点 的圆
的圆 相切,切点为
相切,切点为 .证明:线段
.证明:线段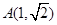 是离心率为
是离心率为 的椭圆
的椭圆 :
: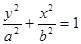
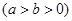 上的一点,斜率为
上的一点,斜率为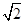 的直线
的直线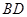 交椭圆
交椭圆 ,
,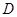 两点,且
两点,且 、
、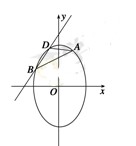
 ,
,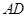 的斜率之和为定值.
的斜率之和为定值. 中,点P到两圆C1与C2的圆心的距离之和等于4,其中C1:
中,点P到两圆C1与C2的圆心的距离之和等于4,其中C1: ,C2:
,C2: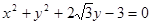 . 设点P的轨迹为
. 设点P的轨迹为 .
. 与C交于A,B两点.问k为何值时
与C交于A,B两点.问k为何值时

 ?此时
?此时 的值是多少?
的值是多少? =1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.
=1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.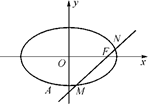
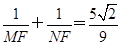 ,求实数m;
,求实数m;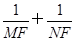 的值是否与θ的大小无关,并证明你的结论.
的值是否与θ的大小无关,并证明你的结论.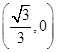 的直线l与曲线E交于点A、B,且
的直线l与曲线E交于点A、B,且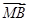 =-2
=-2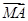 .
. =1(a>b>0)的焦点为F1与F2,且P∈E,∠F1PF2=2θ.求证:△PF1F2的面积S=b2tanθ.
=1(a>b>0)的焦点为F1与F2,且P∈E,∠F1PF2=2θ.求证:△PF1F2的面积S=b2tanθ.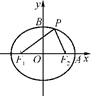
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为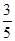 ,且过点P
,且过点P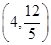 ,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.
,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.