题目内容
已知函数 ,若对于任意
,若对于任意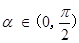 ,都有
,都有 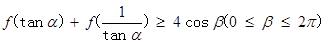 成立,则
成立,则 的取值范围是
的取值范围是
A.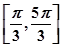 | B.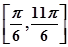 |
C.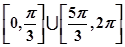 | D.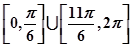 |
A
解析试题分析:根据题意,由于函数 ,若对于任意
,若对于任意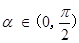
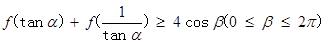 ,则可知
,则可知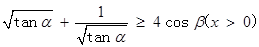 ,那么可知
,那么可知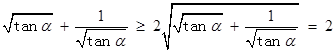 ,因此只要
,因此只要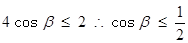 ,结合余弦函数的性质可知,
,结合余弦函数的性质可知, 的取值范围是
的取值范围是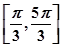 ,故选A
,故选A
考点:函数单调性的运用
点评:解决的关键是利用函数的单调性来结合不等式的性质得到参数的范围。属于中档题。

练习册系列答案
相关题目
函数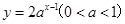 的图象一定过点( )
的图象一定过点( )
| A.(1,1) | B.(1,2) | C.(2,0) | D.(2,-1) |
函数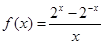 的图象
的图象
| A.关于原点对称 | B.关于y轴对称 | C.关于x轴对称 | D.关于直线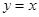 对称 对称 |
下列函数中,周期为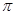 ,且在区间
,且在区间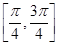 上单调递增的函数是
上单调递增的函数是
A.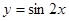 | B.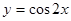 | C.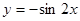 | D.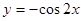 |
如果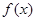 为偶函数,且
为偶函数,且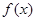 导数存在,则
导数存在,则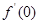 的值为 ( )
的值为 ( )
| A.2 | B.1 | C.0 | D.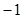 |
当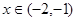 时,不等式
时,不等式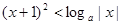 恒成立,则实数
恒成立,则实数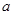 取值范围是( )
取值范围是( )
| A.[2,+∞) | B.(1,2] | C.(1,2) | D.(0,1) |
定义在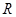 上的可导函数
上的可导函数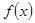 ,已知
,已知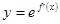 的图像如图所示,则
的图像如图所示,则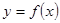 的增区间是( )
的增区间是( )
A.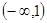 | B. | C.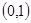 | D.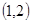 |
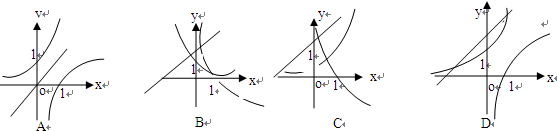
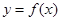 的图象如图1所示,则
的图象如图1所示,则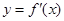 的图象可能是( )
的图象可能是( ) 
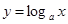 ,
,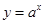 ,y=x+a的图象,可能正确的是
,y=x+a的图象,可能正确的是