题目内容
设甲、乙两套试验方案在一次试验中成功的概率均为p,且这两套试验方案中至少有一套试验成功的概率为0.51,假设这两套试验方案在试验过程中,相互之间没有影响.设试验成功的方案的个数ξ.(1)求p的值;
(2)求ξ的数学期望Eξ与方差Dξ.
【答案】分析:(1)由题意记“这两套试验方案在一次试验中均不成功”的事件为A,利用独立事件同时发生的概率公式及对立事件的定义可以求解;
(2)由题意由于验成功的方案的个数ξ,又随机变量的定义及题意可知ξ的取值为0,1,2,利用独立事件同时发生的概率公式求出该变量的分布列,并代入公式求出期望及方差.
解答:解:(1)记“这两套试验方案在一次试验中均不成功”的事件为A,
则“至少有一套试验成功”的事件为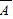 .
.
由题意,这两套试验方案在一次试验中不成功的概率均为1-p.
所以P(A)=(1-p)2,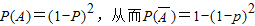 .
.
令1-(1-p)2=0.51,解得p=0.3.
(2)ξ的取值为0,1,2.(7分)P(ξ=0)=(1-0.3)2=0.49,
P(ξ=1)=2×0.3×(1-0.3)=0.42,P(ξ=2)=0.32=0.09.
所以ξ的分布列为
ξ的数学期望Eξ=0×P(ξ=0)+1×P(ξ=1)+2×P(ξ=2)=0.6,
方差Dξ=(0-0.6)2×0.49+(1-0.6)2×0.42+(2-0.6)2×0.09=0.42.
点评:此题考查了离散型随机变量的定义,随机变量的分布列,期望方差及独立事件同时发生的概率.
(2)由题意由于验成功的方案的个数ξ,又随机变量的定义及题意可知ξ的取值为0,1,2,利用独立事件同时发生的概率公式求出该变量的分布列,并代入公式求出期望及方差.
解答:解:(1)记“这两套试验方案在一次试验中均不成功”的事件为A,
则“至少有一套试验成功”的事件为
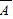 .
.由题意,这两套试验方案在一次试验中不成功的概率均为1-p.
所以P(A)=(1-p)2,
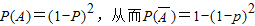 .
.令1-(1-p)2=0.51,解得p=0.3.
(2)ξ的取值为0,1,2.(7分)P(ξ=0)=(1-0.3)2=0.49,
P(ξ=1)=2×0.3×(1-0.3)=0.42,P(ξ=2)=0.32=0.09.
所以ξ的分布列为
| ξ | O | 1 | 2 |
| P | 0.49 | 0.42 | 0.09 |
ξ的数学期望Eξ=0×P(ξ=0)+1×P(ξ=1)+2×P(ξ=2)=0.6,
方差Dξ=(0-0.6)2×0.49+(1-0.6)2×0.42+(2-0.6)2×0.09=0.42.
点评:此题考查了离散型随机变量的定义,随机变量的分布列,期望方差及独立事件同时发生的概率.

练习册系列答案
相关题目