题目内容
ABCD为长方形,AB=4,BC=2,O为AB的中点.在长方形ABCD内随机取一点,取到的点到O的距离小于2的概率为( )
A、1-
| ||
B、1-
| ||
C、
| ||
D、
|
分析:本题利用几何概型解决,这里的区域平面图形的面积.欲求取到的点到O的距离小于2的概率,只须求出圆内的面积与矩形的面积之比即可.
解答:解: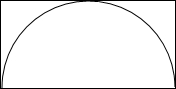 根据几何概型得:
根据几何概型得:
取到的点到O的距离小于2的概率:
p=
=
=
=
.
故选D.
 根据几何概型得:
根据几何概型得:取到的点到O的距离小于2的概率:
p=
| d |
| D |
| 圆内部分的面积 |
| 矩形的面积 |
=
| ||
| 4×2 |
| π |
| 4 |
故选D.
点评:几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=
求解.
| N(A) |
| N |

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
ABCD为长方形,AB=2,BC=1,O为AB的中点,在长方形ABCD内随机取一点,取到的点到O的距离大于1的概率为( )
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
ABCD为长方形,AB=2,BC=1,O为AB的中点,在长方形ABCD内随机取一点,取到的点到O的距离大于1的概率为( )
A、1-
| ||
| B、1 | ||
C、1+
| ||
D、
|
 B.
B. C.
C. D.
D.