题目内容
【题目】综合题
(1)已知α为第二象限角,且 sinα= ![]() ,求
,求 ![]() 的值.
的值.
(2)已知α∈(0, ![]() ),β∈(0,π),且tan(α﹣β)=
),β∈(0,π),且tan(α﹣β)= ![]() ,tanβ=﹣
,tanβ=﹣ ![]() ,求tan(2α﹣β)的值及角2α﹣β.
,求tan(2α﹣β)的值及角2α﹣β.
【答案】
(1)解:∵已知α为第二象限角,且 sinα= ![]() ,∴cosα=﹣
,∴cosα=﹣ ![]() =﹣
=﹣ ![]() ,
,
∴ ![]() =
= ![]() =
= 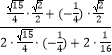 =﹣
=﹣ ![]()
(2)解:∵已知α∈(0, ![]() ),β∈(0,π),且tan(α﹣β)=
),β∈(0,π),且tan(α﹣β)= ![]() ,tanβ=﹣
,tanβ=﹣ ![]() ,
,
∴β∈( ![]() ,π),α﹣β∈(﹣π,﹣
,π),α﹣β∈(﹣π,﹣ ![]() ),2α﹣β∈(﹣π,0).
),2α﹣β∈(﹣π,0).
∵tan(2α﹣2β)= ![]() =
= ![]() >1,
>1,
∴tan(2α﹣β)=tan[(2α﹣2β)+β]= ![]() =
= 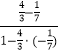 =1,
=1,
∴2α﹣β=﹣ ![]()
【解析】(1)利用同角三角函数的基本关系求得cosα的值,再利用两角和差的三角公式求得要求式子的值.(2)利用两角和差的三角公式求得 tan(2α﹣β)=tan[(2α﹣2β)+β]的值,再结合2α﹣β的范围,求得2α﹣β的值.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
【题目】某港口的水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下面是每天时间与水深的关系表:
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 10 | 13 | 9.9 | 7 | 10 | 13 | 10.1 | 7 | 10 |
经过长期观测,y=f(t)可近似的看成是函数y=Asinωt+b
(1)根据以上数据,求出y=f(t)的解析式;
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?