题目内容
某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.
但国家每天分配给该厂的煤、电有限, 每天供煤至多56吨,供电至多450千瓦,问该厂如何安排生产,使得该厂日产值最大?最大日产值为多少?
该厂每天安排生产甲产品5吨,乙产品7吨,可得日产值为z的最大值为124万元.
解析试题分析:根据已知条件列出线性约束条件,和目标函数。画出可行域与目标函数线,平移目标函数线使之经过可行域,当目标函数线纵截距最大时目标函数值也最大。
试题解析:
解:设该厂每天安排生产甲产品x吨,乙产品y吨,日产值为z,可得
z=8x+12y, 2分
其中x、y满足约束条件 5分
5分
作出可行域,如图所示 7分
将直线l:z=8x+12y进行平移,由图可知当直线l经过可行域上的点M时,
直线在y轴上的截距最大,目标函数z同时达到最大值 10分
解方程组 ,得M(5,7) 12分
,得M(5,7) 12分
∴z的最大值为zmax=8×5+12×7=124
答:该厂每天安排生产甲产品5吨,乙产品7吨,可得日产值为z的最大值为124万元. 14分
考点:线性规划。

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
不等式 的解集是
的解集是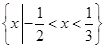 ,则
,则 ( )
( )
A. | B. | C.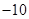 | D. |
已知实数a,b,c满足b+c=6-4a+3a2,c-b=4-4a+a2,则a,b,c的大小关系
是 ( )
| A.a>c≥b | B.c≥b>a |
| C.c>b>a | D.a>c>b |
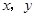 满足
满足 则
则 的最大值是_______
的最大值是_______ 中,已知点
中,已知点 ,
, ,
, ,点
,点 在
在 三边围成的区域(含边界)上,且
三边围成的区域(含边界)上,且 .
. ,求
,求 ;
;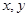 表示
表示 ,并求
,并求
 x-y+
x-y+ 个单位的碳水化合物,
个单位的碳水化合物, 个单位的蛋白质和
个单位的蛋白质和 ;一个单位的晚餐含
;一个单位的晚餐含 个单位的碳水化合物,
个单位的碳水化合物, 个单位的维生素
个单位的维生素 个单位的碳水化合物,
个单位的碳水化合物, 个单位的蛋白质和
个单位的蛋白质和 个单位的维生素
个单位的维生素 元和
元和 元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐? 则
则 的最大值是 ▲ 。
的最大值是 ▲ 。