题目内容
已知 是R上奇函数
是R上奇函数(I)求a,b的值;
(II)解不等式
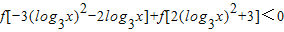 .
.
【答案】分析:(I)由奇函数的性质可得f(0)=0,解得b=-1,再由 f(-1)=-f(1),求出a的值.
(II)由于f(x) 在R上是单调增函数,故不等式等价于 ,解得 log3x 的范围,再解对数不等式即可求得原不等式的解集.
,解得 log3x 的范围,再解对数不等式即可求得原不等式的解集.
解答:解:(I)∵已知 是R上奇函数,故有f(0)=0,解得b=-1.
是R上奇函数,故有f(0)=0,解得b=-1.
又∵f(-1)=-f(1),∴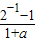 =-
=-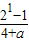 ,解得 a=2.
,解得 a=2.
此时,f(x)= ,经过检验,此函数为奇函数.
,经过检验,此函数为奇函数.
(II)∵f(x)= -
-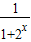 ,故函数在R上是单调增函数,故不等式等价于
,故函数在R上是单调增函数,故不等式等价于
 ,
, +2log3x-3>0,
+2log3x-3>0,
解得 log3x<-3,或 log3x>1,即 0<x<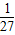 ,或 x>3,
,或 x>3,
故不等式的解集为 {x|0<x<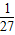 ,或 x>3 }.
,或 x>3 }.
点评:本题主要考查对数函数的图象和性质、以及奇函数的性质、函数的单调性的综合应用,一元二次不等式、对数不等式的解法,属于中档题.
(II)由于f(x) 在R上是单调增函数,故不等式等价于
 ,解得 log3x 的范围,再解对数不等式即可求得原不等式的解集.
,解得 log3x 的范围,再解对数不等式即可求得原不等式的解集.解答:解:(I)∵已知
 是R上奇函数,故有f(0)=0,解得b=-1.
是R上奇函数,故有f(0)=0,解得b=-1.又∵f(-1)=-f(1),∴
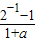 =-
=-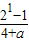 ,解得 a=2.
,解得 a=2.此时,f(x)=
 ,经过检验,此函数为奇函数.
,经过检验,此函数为奇函数.(II)∵f(x)=
 -
-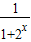 ,故函数在R上是单调增函数,故不等式等价于
,故函数在R上是单调增函数,故不等式等价于 ,
, +2log3x-3>0,
+2log3x-3>0,解得 log3x<-3,或 log3x>1,即 0<x<
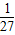 ,或 x>3,
,或 x>3,故不等式的解集为 {x|0<x<
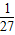 ,或 x>3 }.
,或 x>3 }.点评:本题主要考查对数函数的图象和性质、以及奇函数的性质、函数的单调性的综合应用,一元二次不等式、对数不等式的解法,属于中档题.

练习册系列答案
相关题目
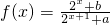 是R上奇函数
是R上奇函数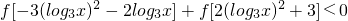 .
. 是R上奇函数
是R上奇函数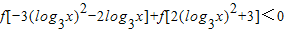 .
.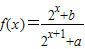 是R上奇函数
是R上奇函数 .
. 是R上奇函数
是R上奇函数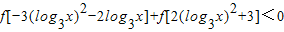 .
.