题目内容
3.已知点A(a,0),B(b,0),则向量|$\overrightarrow{AB}$|=( )| A. | |a-b| | B. | a-b | C. | b-a | D. | $\sqrt{{a}^{2}+{b}^{2}}$ |
分析 由题意可得向量$\overrightarrow{AB}$的坐标,然后由向量的模长公式可得.
解答 解:由题意可得:$\overrightarrow{AB}$向量的坐标为:(a,0)-(b,0)=(a-b,0),
由模长公式可得:|$\overrightarrow{AB}$|=$\sqrt{(a-b)^{2}}$=|a-b|,
故选:A.
点评 本题考查向量的模长公式,涉及向量的坐标运算,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.存在实数x使得不等式|x+3|+|x-1|≤22a-3•2a成立,则实数a的取值范围为( )
| A. | (-∞,-1]∪[4,+∞) | B. | [2,+∞) | C. | [1,2] | D. | (-∞,1]∪[2,+∞) |
18.设点A为抛物线y2=4x上一点B(1,0),且AB=1,则A的横坐标的值( )
| A. | -2 | B. | 0 | C. | -2或0 | D. | -2或2 |
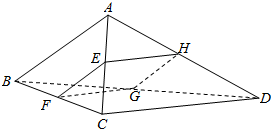 如图,在空间四边形ABCD中,AC,BD为其对角线,E,F,G,H分别为AC,BC,BD,AD上的点,若四边形EFGH为平行四边形,求证:AB∥平面EFGH.
如图,在空间四边形ABCD中,AC,BD为其对角线,E,F,G,H分别为AC,BC,BD,AD上的点,若四边形EFGH为平行四边形,求证:AB∥平面EFGH.