题目内容
 已知
已知| a |
| b |
| a |
| 3 |
| b |
| a |
| 3 |
| b |
(1)求点P(x,y)的轨迹C的方程,且画出轨迹C的草图;
(2)若直线l:y=kx+m(k≠0)与上述曲线C交于不同的两点A、B,求实数k和m所满足的条件;
(3)在(2)的条件下,若另有定点D(0,-1),使|AD|=|BD|,试求实数m的取值范围.
分析:(1)利用几何条件(
+
)•(
-
)=0列方程,即可求得点P(x,y)的轨迹C的方程,画图时注意:不画渐近线不得分
(2)将直线方程代入曲线方程,所得一元二次方程二次项系数不为零,判别式△>0,列不等式即可得实数k和m所满足的条件;
(3)设出A、B的坐标,利用韦达定理,可得AB中点H的坐标(用k、m表示),因为|AD|=|BD|,所以AB⊥DH,kAB•kDH=-1,即可得k与m的等量关系,进而利用k的范围求得m的范围.
| a |
| 3 |
| b |
| a |
| 3 |
| b |
(2)将直线方程代入曲线方程,所得一元二次方程二次项系数不为零,判别式△>0,列不等式即可得实数k和m所满足的条件;
(3)设出A、B的坐标,利用韦达定理,可得AB中点H的坐标(用k、m表示),因为|AD|=|BD|,所以AB⊥DH,kAB•kDH=-1,即可得k与m的等量关系,进而利用k的范围求得m的范围.
解答: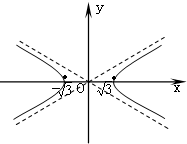 解:(1)(
解:(1)(
+
)⊥(
-
)⇒(
+
)•(
-
)=0
⇒
2=3
2⇒x2=3(y2+1)
∴P(x,y)的轨迹C的方程为
-y2=1
其草图如右. (注:不画渐近线,不得分)
(2)
⇒(1-3k2)x2-6kmx-3m2-3=0
⇒
(*)
(3)设A(x1,y1)、B(x2,y2),A、B中点为H(x0,y0),
则x0=
=
,y0=kx0+m=
,
由题意,有AB⊥DH⇒kAB•kDH=-1
⇒k•
=-1 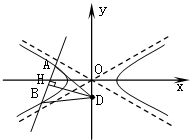
⇒3k2=4m+1,
代入(*),得
⇒-
<m<0或m>4.
 解:(1)(
解:(1)(| a |
| 3 |
| b |
| a |
| 3 |
| b |
| a |
| 3 |
| b |
| a |
| 3 |
| b |
⇒
| a |
| b |
∴P(x,y)的轨迹C的方程为
| x2 |
| 3 |
其草图如右. (注:不画渐近线,不得分)
(2)
|
|
|
(3)设A(x1,y1)、B(x2,y2),A、B中点为H(x0,y0),
则x0=
| x1+x2 |
| 2 |
| 3km |
| 1-3k2 |
| m |
| 1-3k2 |
由题意,有AB⊥DH⇒kAB•kDH=-1
⇒k•
| ||
|

⇒3k2=4m+1,
代入(*),得
|
⇒-
| 1 |
| 4 |
点评:本题综合考查了曲线与方程,直线与双曲线的关系,特别是直线与双曲线的相交情形,解题时要善于将几何条件转化为代数条件,用代数方法解决几何问题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目