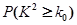题目内容
从高二(1)班6名男生和3名女生中选出4人组成代表队,参加学校辩论比赛,如果男生中的甲和女生中的乙必须在内,则共有选法种数是( )
分析:由题意,只需从其余7名学生中产生两名代表即可.
解答:解:由题意,只需从其余7名学生中产生两名代表,即
=21种,
故选B.
| C | 2 7 |
故选B.
点评:本题考查组合知识,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
(本小题满分12分)在第9届校园文化艺术节棋类比赛项目报名过程中,我校高二(2)班共有16名男生和14名女生预报名参加,调查发现,男、女选手中分别有10人和6人会围棋.
(I)根据以上数据完成以下2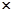 2列联表:
2列联表:
|
|
会围棋 |
不会围棋 |
总计 |
|
男 |
|
|
|
|
女 |
|
|
|
|
总计 |
|
|
30 |
并回答能否在犯错的概率不超过0.10的前提下认为性别与会围棋有关?
参考公式: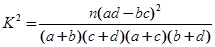 其中n=a+b+c+d
其中n=a+b+c+d
参考数据:
|
|
0.40 |
0.25 |
0.10 |
0.010 |
|
|
0.708 |
1.323 |
2.706 |
6.635 |
(Ⅱ)若从会围棋的选手中随机抽取3人成立该班围棋代表队,则该代表队中既有男又
有女的概率是多少?
(Ⅲ)若从14名女棋手中随机抽取2人参加棋类比赛,记会围棋的人数为 ,求
,求 的期望.
的期望.