题目内容
某人用一颗骰子(各面上分别标以1到6的均匀正方体玩具)做抛掷得分游戏,规则如下:若抛出的点数为3的倍数,则得1分,否则得-1分.(I)求抛掷1次恰好得1分的概率;
(II)求抛掷4次至少得2分的概率.
【答案】分析:(I)由题意知这是一个古典概型,可以列举出试验发生包含的所以投事件数是6,而满足条件的事件数是2,根据古典概型的概率公式得到结果.
(II)抛掷4次至少得(2分),包括得4次中A发生3次和4次两种情形,这两种情形是互斥的,分别表示出两种情形的概率,用互斥事件的概率公式得到结果.在计算每一种情形时,要用到独立重复试验的概率公式.
解答:解:(I)由题意知这是一个古典概型,
∵试验发生包含的所以投事件数是6,
而满足条件的事件数是2
设“设抛掷一颗骰子掷出的点数为3的倍数”为事件A.
∴抛掷1次得(1分)的概率为 .
.
(II)抛掷4次至少得(2分),包括得4次中A发生3次和4次两种情形:
若4次中A发生3次,则得到(2分),其概率为: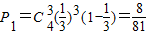
若4次中A发生4次,则得到(4分),其概率为:
故抛掷4次至少得(2分)的概率为: .
.
点评:本题考查独立重复试验,古典概型,互斥事件的概率公式,是一个综合题,解题时注意弄清题意,代入公式时不要弄错数字,一般不会丢分.
(II)抛掷4次至少得(2分),包括得4次中A发生3次和4次两种情形,这两种情形是互斥的,分别表示出两种情形的概率,用互斥事件的概率公式得到结果.在计算每一种情形时,要用到独立重复试验的概率公式.
解答:解:(I)由题意知这是一个古典概型,
∵试验发生包含的所以投事件数是6,
而满足条件的事件数是2
设“设抛掷一颗骰子掷出的点数为3的倍数”为事件A.
∴抛掷1次得(1分)的概率为
 .
.(II)抛掷4次至少得(2分),包括得4次中A发生3次和4次两种情形:
若4次中A发生3次,则得到(2分),其概率为:
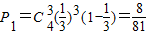
若4次中A发生4次,则得到(4分),其概率为:

故抛掷4次至少得(2分)的概率为:
 .
.点评:本题考查独立重复试验,古典概型,互斥事件的概率公式,是一个综合题,解题时注意弄清题意,代入公式时不要弄错数字,一般不会丢分.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目